已知A=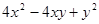 ,B=
,B=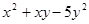 ,求(3A-2B)-(2A+B)的值。
,求(3A-2B)-(2A+B)的值。
先填空再解答:
某村去年种植的油菜籽亩产量达150千克,含油率为40%.今年改种新选育的油菜籽后亩产量提高了30千克,含油率提高了10百分点.今年与去年相比,油菜的种植面积减少了40亩,而村榨油厂用本村所产油菜籽的产油量提高了20%.
(1)求今年油菜的种植面积.
设今年油菜的种植面积是x亩.完成下表后再列方程解答;
(2)已知油菜种植成本为200元/亩,菜油收购价为6元/千克.试比较这个村去今两年种植油菜的纯收入.
如图1,射线OC、OD在∠AOB的内部,且∠AOB=150°,∠COD=30°,射线OM、ON分别平分∠AOD、∠BOC,
(1)求∠MON的大小,并说明理由;
(2)如图2,若∠AOC=15°,将∠COD绕点O以每秒x°的速度逆时针旋转10秒钟,此时∠AOM︰∠BON=7︰11,如图3所示,求x的值.
若(6m-1)2与|4n+2|互为相反数,那么多项式6mx2+2y+2xy-(x2-4nxy)的值与x的取值有无关系?说出你的理由.
在平整的地面上,有若干个完全相同的棱长为10cm的小正方体堆成一个几何体,如图所示。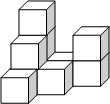
(1)这个几何体由个小正方体组成,请画出这个几何体的三视图。
主视图左视图俯视图
(2)如果在这个几何体的表面喷上黄色的漆,则在所有的小正方体中,有个正方体只有一个面是黄色,有个正方体只有两个面是黄色,有个正方体只有三个面是黄色。
(3)若现在你手头还有一些相同的小正方体,如果保持俯视图和左视图不变,最多可以再添加几个小正方体?这时如果要重新给这个几何体表面喷上红漆,需要喷漆的面积比原几何体增加还是减少了?增加或减少了多少cm2?
为丰富学生的课余生活,陶冶学生的情趣和爱好,重庆一中初2012级开展了学生社团活动.年级为了解学生分类参加情况,进行了抽样调查,制作出如下的统计图.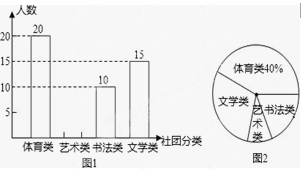
请根据上述统计图,完成以下问题:
(1)写出上述统计图中图1的名称是;
(2)这次共调查了名学生;参加文学类学生所占的百分比为;在扇形统计
图中,表示“书法类”所在扇形的圆心角是度;
(3)请把统计图1补充完整;
(4)若初2012级共有学生1100名,请估算有多少名学生参加文学类社团?