已知二次函数图象的顶点坐标为,该二次函数图象的对称轴与轴的交点为,是这个二次函数图象上的点,是原点.
(1)不等式是否成立?请说明理由;
(2)设是的面积,求满足的所有点的坐标.
(8分)在□ABCD中,E、F分别是AB、CD的中点,连接AF、CE.
(1)求证:△BEC≌△DFA;
(2)连接AC,当CA=CB时,判断四边形AECF是什么特殊四边形?并证明你的结论.
(8分)某企业为了改善 污水处理条件,决定购买A、B两种型号的污水处理设备
污水处理条件,决定购买A、B两种型号的污水处理设备
共8台,其中每台的价格、月处理污水量如下表:
经预算,企业最多支出57万元购买污水处理设备,
且要求设备月处理污水量不低于1490吨.
(1)企业有哪几种购买方案?
(2)哪种购买方案更省钱?
(6分)某商场准备改善原有楼梯的安 全性能,把倾斜角由原来的40º减至35º.已
全性能,把倾斜角由原来的40º减至35º.已
知原楼梯AB长为5m,调整后的楼梯所占地面CD有多长?(结果精确到0.1m.参考数据:
sin40º≈0.64,cos40º≈0.77,sin35º≈0.57,tan35º≈0.70)
(6分)小明和小亮用图中的转盘做游戏:分别转动转盘两次,若两次数字之差(大
数减小数)大于或等于2,小明得1分,否则小亮得1分.你认为游戏是否公平?若公平,
请说明理由 ;若不公平,请你修改规则,使游戏对双方公平.
;若不公平,请你修改规则,使游戏对双方公平.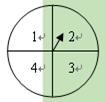
(6分)图1是某城市三月份1至8日的日最高气温随时间变化的折线统计图,小
刚根据图1将数据统计整理后制成了图2.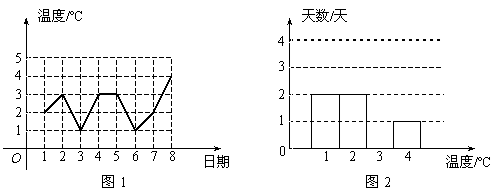
根据图中信息,解答下列问题:
(1)将图2补充完整;
(2)这8天的日最高气温的中位数是 ºC;
(3)计算这8天的日最高气温的平均数.