求两直线L1:4x-3y+1=0和L2:12x+5y+13=0夹角平分线方程
某造船公司年造船量是20艘,已知造船x艘的产值函数为R(x)=3700x+45x2-10x3(单位:万元),成本函数为C(x)=460x+5000(单位:万元),又在经济学中,函数f(x)的边际函数Mf(x)定义为Mf(x)=f(x+1)-f(x).
(1)求利润函数P(x)及边际利润函数MP(x);(提示:利润=产值-成本)
(2)问年造船量安排多少艘时,可使公司造船的年利润最大?
已知 的展开式中偶数项二项式系数和比
的展开式中偶数项二项式系数和比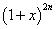 展开式中奇数项二项式系数和小
展开式中奇数项二项式系数和小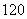 ,求:
,求:
(I)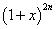 展开式中二项式系数最大的项;
展开式中二项式系数最大的项;
(II)设 展开式中的常数项为p,展开式中所有项系数的和为q,求p+q.
展开式中的常数项为p,展开式中所有项系数的和为q,求p+q.
已知关于x的一元二次方程x2-2(a-2)x-b2+16=0.
(1)若a,b是一枚骰子掷两次所得到的点数,求方程有两正根的概率;
(2)若a∈[2,6],b∈[0,4],求方程没有实根的概率.
用0,1,2,3,4,5这六个数字(允许重复),组成四位数.
( I)可以组成多少个四位数?
( II)可组成多少个恰有两个相同数字的四位数?
设函数
(Ⅰ)当 时,求函数
时,求函数 的极值;
的极值;
(Ⅱ)当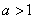 时,讨论函数
时,讨论函数 的单调性.
的单调性.
(Ⅲ)若对任意 及任意
及任意 ,恒有
,恒有 成立,求实数
成立,求实数 的取值范围.
的取值范围.