连接上海市区到浦东国际机场的磁悬浮轨道全长约为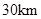
，列车走完全程包含启动加速、匀速运行、制动减速三个阶段．已知磁悬浮列车从启动加速到稳定匀速动行共需
秒，在这段时间内记录下下列数据：
（1）请你在一次函数、二次函数和反比例函数中选择合适的函数来分别表示在加速阶段（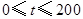
）速度
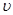与时间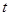
的函数关系、路程
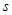与时间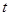的函数关系．
（2）最新研究表明，此种列车的稳定动行速度可达180米／秒，为了检测稳定运行时各项指标，在列车达到这一速度后至少要运行100秒，才能收集全相关数据．若在加速过程中路程、速度随时间的变化关系仍然满足（1）中的函数关系式，并且制作减速所需路程与启动加速的路程相同．根据以上要求，至少还要再建多长轨道就能满足试验检测要求？
（3）若减速过程与加速过程完全相反．根据对问题（2）的研究，直接写出列车在试验检测过程中从启动到停车这段时间内，列车离开起点的距离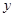
（米）与时间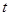（秒）的函数关系式（不需要写出过程）
求证：有一组对边平行，和一组对角相等的四边形是平行四边形．（请画出图形，写出已知、求证并证明）
2010年春季我国西南五省持续干旱，旱情牵动着全国人民的心。“一方有难、八方支援”，某厂计划生产1800吨纯净水支援灾区人民，为尽快把纯净水发往灾区，工人把每天的工作效率提高到原计划的1.5倍，结果比原计划提前3天完成了生产任务．求原计划每天生产多少吨纯净水？
先化简，再求值：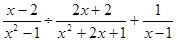
，其中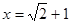
．
解分式方程：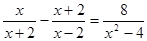 
.
如图，在四边形纸片ABCD中，已知：AD∥BC，AB∥CD，∠B=90°，现将四边形纸片ABCD对折，折痕为PF（点P在BC上，点F在DC上），使顶点C落在四边形ABCD内一点C′，PC′的延长线交AD于M，再将纸片的另一部分对折（折痕为ME），使顶点A落在直线PM上一点A′.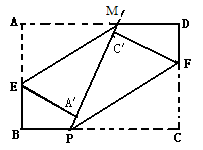
（1）填空：
因为AD∥BC，（已知）
所以∠B+∠A=180°（）
又因为∠B=90°（已知）
所以∠A=度.
则：∠EA′M=度.
又因为AB∥CD（已知）
同理：∠FC′P=∠C=度.
所以∠EA′M ∠FC′P（填 “＜”或“=”或“＞”）
所以∥理由：（）.
（2）ME与PF平行吗？请说明理由.