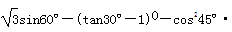已知二次函数图像与y轴交于点(0,-4),并经过(-1,-6)和(1,2)
(1)求这个二次函数的解析式;
(2)求出这个函数的图像的开口方向,对称轴和顶点坐标;
(3)该函数图像与x轴的交点坐标 .
如图,已知直线PA交⊙O于A、B两点,AE是⊙O的直径.点C为⊙O上一点,且AC平分∠PAE,过C作CD⊥PA,垂足为D.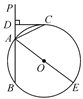
(1)求证:CD为⊙O的切线;
(2)若DC+DA=6,⊙O的直径为10,求AB的长度.
关于x的方程  ,
,
(1)a为何值时,方程的一根为0?
(2)a为何值时,两根互为相反数?
某篮球队运动员进行3分球投篮成绩测试,每人每天投3分球10次,对甲、乙两名队员在5天中进球的个数统计如果如下:
| 队员 |
每人每天进球数 |
||||
| 甲 |
10 |
6 |
10 |
8 |
8 |
| 乙 |
9 |
9 |
7 |
8 |
9 |
经计算,甲进球的平均数为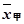 =8.4和方差s甲2="2.24."
=8.4和方差s甲2="2.24."
(1)求乙进球的平均数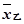 和方差s乙2;
和方差s乙2;
(2)现在需要根据以上结果,从甲、乙二人中选出一人去参加3分球投篮大赛,你认为应该选哪名队员?为什么?
解下列方程(每小题4分,共8分)
(1)(x+1)2=4 (2)x(x-6)=6.
化简与计算(每小题4分,共8分)
(1)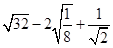 ;(2)化简:
;(2)化简: