已知A、B、C是椭圆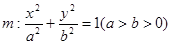 上的三点,其中点A的坐标为
上的三点,其中点A的坐标为 ,BC过椭圆m的中心,且
,BC过椭圆m的中心,且
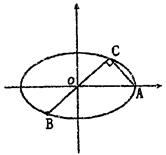
(1)求椭圆 的方程;
的方程;
(2)过点 的直线l(斜率存在时)与椭圆m交于两点P,Q,
的直线l(斜率存在时)与椭圆m交于两点P,Q,
设D为椭圆m与y轴负半轴的交点,且 ,求实数t的取值范围.
,求实数t的取值范围.
.
已知函数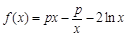 .
.
⑴若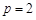 ,求曲线
,求曲线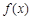 在点
在点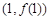 处的切线方程;
处的切线方程;
⑵若函数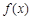 在其定义域内为增函数,求正实数
在其定义域内为增函数,求正实数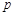 的取值范围;
的取值范围;
调查某初中1000名学生的肥胖情况,得下表:
| 偏瘦 |
正常 |
肥胖 |
|
| 女生(人) |
100 |
173 |
 |
| 男生(人) |
 |
177 |
 |
已知从这批学生中随机抽取1名学生,抽到偏瘦男生的概率为0.15。
(1)求 的值;
的值;
(2)若用分层抽样的方法,从这批学生中随机抽取50名,问应在肥胖学生中抽多少名?
(3)已知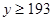 ,
, ,肥胖学生中男生不少于女生的概率。
,肥胖学生中男生不少于女生的概率。
(本小题满分12分)下图是一几何体的直观图、主视图、俯视图、左视图.
(1)若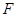 为
为 的中点,求证:
的中点,求证: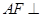 面
面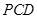 ;
;
(2)求A到面PEC的距离;
.(本小题满分12分)如图某河段的两岸可视为平行,为了测量该河段的宽度,在河段的一岸边选取两点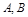 ,观察对岸的点
,观察对岸的点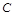 ,测得
,测得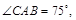
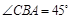 ,且
,且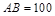 米.
米.
(1)求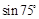 ;
;
(2)求该河段的宽度.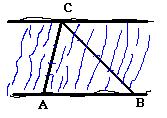
.(本小题满分14分)已知函数f (x)=lnx,g(x)=ex.
( I)若函数φ (x) = f (x)- ,求函数φ (x)的单调区间;
,求函数φ (x)的单调区间;
(Ⅱ)设直线l为函数的图象上一点A(x0,f (x0))处的切线.证明:在区间(1,+∞)上存在唯一的x0,使得直线l与曲线y=g(x)相切.