如图,已知等边△ABC中,D、E两点在直线BC上,且∠DAE=120°.
⑴判断△ABD是否与△ECA相似,并说明你的理由;
⑵当CE·BD=16时,求△ABC的周长.
某商店销售10台A型和20台B型电脑的利润为4000元,销售20台A型和10台B型电脑的利润为3500元.
(1)求每台A型电脑和B型电脑的销售利润;
(2)该商店计划一次购进两种型号的电脑共100台,其中B型电脑的进货量不超过A型电脑的2倍,设购进A型电脑x台,这100台电脑的销售总利润为y元.
①求y关于x的函数关系式;
②该商店购进A型、B型电脑各多少台,才能使销售总利润最大?
(3)实际进货时,厂家对A型电脑出厂价下调m(0<m<100)元,且限定商店最多购进A型电脑70台,若商店保持同种电脑的售价不变,请你根据以上信息及(2)中条件,设计出使这100台电脑销售总利润最大的进货方案.
在梯形ABCD中,AD∥BC,∠D=90°,以AB为直径作⊙O.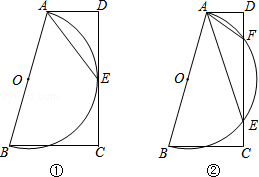
(1)如图①,⊙O与DC相切于点E,
①求证:∠BAE=∠DAE;②若AB=6,求AD+BC的值.
(2)如图②,⊙O与DC交于点E、F.
①图中哪一个角与∠BAE相等?为什么?②试探究线段DF与CE的数量关系,并说明理由.
如图,已知AB是⊙O的直径,点C在⊙O上,过点C的直线与AB的延长线交于点P,AC=PC,∠COB=2∠PCB.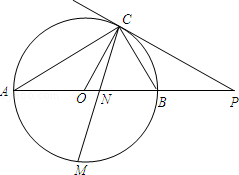
(1)求证:PC是⊙O的切线;
(2)求证:BC=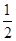 AB;
AB;
(3)点M是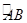 的中点,CM交AB于点N,若AB=4,求MN•MC的值.
的中点,CM交AB于点N,若AB=4,求MN•MC的值.
在中俄“海上联合﹣2014”反潜演习中,我军舰A测得潜艇C的俯角为30°,位于军舰A正上方1000米的反潜直升机B测得潜艇C的俯角为68°,试根据以上数据求出潜艇C离开海平面的下潜深度.(结果保留整数,参考数据:sin68°≈0.9,cos68°≈0.4,tan68°≈2.5,
 1.7)
1.7)
为鼓励创业,市政府制定了小型企业的优惠政策,许多小型企业应运而生,某镇统计了该镇1﹣5月新注册小型企业的数量,并将结果绘制成如下两种不完整的统计图: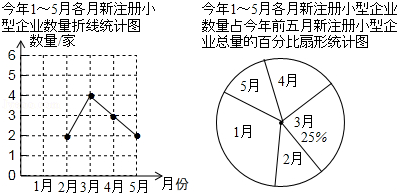
(1)某镇今年1﹣5月新注册小型企业一共有 家.请将折线统计图补充完整;
(2)该镇今年3月新注册的小型企业中,只有2家是餐饮企业,现从3月新注册的小型企业中随机抽取2家企业了解其经营状况,请用列表或画树状图的方法求出所抽取的2家企业恰好都是餐饮企业的概率.