有一边长为 的正方形铁片,铁片的四角截去四个边长为
的正方形铁片,铁片的四角截去四个边长为 的小正方形,然后做成一个无盖方盒。
的小正方形,然后做成一个无盖方盒。
(1)试把方盒的容积 表示成
表示成 的函数;
的函数;
(2)求 多大时,做成方盒的容积
多大时,做成方盒的容积 最大。
最大。
已知函数y=f(x)的定义域为R,且对任意a,b∈R,都有f(a+b)=f(a)+f(b),且当x>0时,f(x)<0恒成立,f(3)="-3."
(1)证明:函数y=f(x)是R上的减函数;
(2)证明:函数y=f(x)是奇函数;
(3)试求函数y=f(x)在[m,n](m,n∈Z)上的值域.
判断下列各函数的奇偶性:
(1)f(x)=(x-2)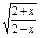 ;
;
(2)f(x)= ;
;
(3)f(x)=
已知函数f(x)的定义域为R,且满足f(x+2)=-f(x).
(1)求证:f(x)是周期函数;
(2)若f(x)为奇函数,且当0≤x≤1时,f(x)= x,求使f(x)=-
x,求使f(x)=- 在[0,2 009]上的所有x的个数.
在[0,2 009]上的所有x的个数.
已知函数f(x),当x,y∈R时,恒有f(x+y)=f(x)+f(y).
(1)求证:f(x)是奇函数;
(2)如果x∈R+,f(x)<0,并且f(1)=- ,试求f(x)在区间[-2,6]上的最值.
,试求f(x)在区间[-2,6]上的最值.
判断下列函数的奇偶性.
(1)f(x)= ;
;
(2)f(x)=log2(x+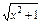 ) (x∈R);
) (x∈R);
(3)f(x)=lg|x-2|.