一个容量为M的样本数据,其频率分布表如下.
(Ⅰ)表中a= ,b = ;
(Ⅱ)画出频率分布直方图;
(Ⅲ)用频率分布直方图,求出总体的众数及平均数的估计值. 频率分布表
频率分布表
| 分组 |
频数 |
频率 |
频率/组距 |
| (10,20] |
2 |
0.10 |
0.010 |
| (20,30] |
3 |
0.15 |
0.015 |
| (30,40] |
4 |
0.20 |
0.020 |
| (40,50] |
a |
b |
0.025 |
| (50,60] |
4 |
0.20 |
0 .020 .020 |
(60, 70] 70] |
2 |
0.10 |
0.010 |
一个口袋内装有大小相同的5 个球,其中3个白球分别记为A1、A2、A3;2个黑
球分别记为B1、B2,从中一次摸出2个球.
(Ⅰ)写出所有的基本事件;
(Ⅱ)求摸出2球均为白球的概率.
某网站欲调查网民对当前网页的满意程度,在登录的所有网民中,收回有效帖子
50000份,其中持各种态度的份数如下表所示.
很满 意 意 |
满意 |
一般 |
不满意 |
| 10800 |
12400 |
15600 |
11200 |
为了调查网民的具体想法和意见,以便决定如何更改才能使网页更完美,打算从中抽选500份,为使样本更具有代表性,每类帖子中各应抽选出多少份?
(本小题满分14分)
已知数列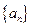 的前
的前 项和是
项和是 ,且
,且 .
.
(Ⅰ) 求证:数列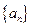 是等比数列;
是等比数列;
(Ⅱ) 记 ,求
,求 的前
的前 项和
项和 的最大值及相应的
的最大值及相应的 值.
值.
(本小题满分14分)
已知函数 的最小正周期为
的最小正周期为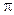 .
.
(Ⅰ)求 的值; (Ⅱ)求函数
的值; (Ⅱ)求函数 的单调递增区间及其图象的对称轴方程.
的单调递增区间及其图象的对称轴方程.