(本小题8分)机器按照模具生产的产品也会有缺陷,我们将有缺陷的产品称为次品,每小时出现的次品数随机器运转速度的不同而变化.下表为某机器生产过程的数据:
| 速度x(百转/秒) |
2 |
4 |
5 |
6 |
8 |
| 每小时生产次品数y(个) |
30 |
40 |
50 |
60 |
70 |
(1)求机器运转速度与每小时生产的次品数之间的回归方程;
(2)若实际生产所允许的每小时生产的次品数不超过75件,那么机器的速度(百转/秒)不超过多少?(写出满足题目的整数解)
在等比数列 中,
中, ,且
,且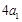 ,
, ,
, 成等差数列.
成等差数列.
(1)求 ;
;
(2)令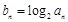 ,求数列
,求数列 的前
的前 项和
项和 .
.
已知点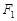 、
、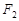 为双曲线
为双曲线 :
:
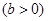 的左、右焦点,过
的左、右焦点,过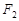 作垂直于
作垂直于 轴的直线,在
轴的直线,在 轴上方交双曲线
轴上方交双曲线 于点
于点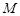 ,且
,且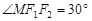 ,圆
,圆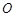 的方程是
的方程是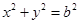 .
.
(1)求双曲线 的方程;
的方程;
(2)过双曲线 上任意一点
上任意一点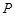 作该双曲线两条渐近线的垂线,垂足分别为
作该双曲线两条渐近线的垂线,垂足分别为 、
、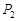 ,求
,求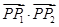 的值;
的值;
(3)过圆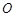 上任意一点
上任意一点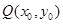 作圆
作圆 的切线
的切线 交双曲线
交双曲线 于
于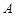 、
、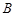 两点,
两点,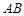 中点为
中点为 ,求证:
,求证: .
.
定义:我们把椭圆的焦距与长轴的长度之比即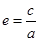 ,叫做椭圆的离心率.若两个椭圆的离心率
,叫做椭圆的离心率.若两个椭圆的离心率 相同,称这两个椭圆相似.
相同,称这两个椭圆相似.
(1)判断椭圆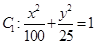 与椭圆
与椭圆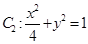 是否相似?并说明理由;
是否相似?并说明理由;
(2)若椭圆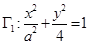
 与椭圆
与椭圆 相似,求
相似,求 的值;
的值;
(3)设动直线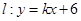 与(2)中的椭圆
与(2)中的椭圆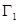 交于
交于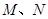 两点,试探究:在椭圆
两点,试探究:在椭圆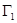 上是否存在异于
上是否存在异于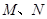 的定点
的定点 ,使得直线
,使得直线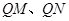 的斜率之积为定值?若存在,求出定点
的斜率之积为定值?若存在,求出定点 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
如图,圆柱的轴截面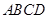 为正方形,
为正方形,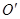 、
、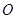 分别为上、下底面的圆心,
分别为上、下底面的圆心,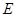 为上底面圆周上一点,已知
为上底面圆周上一点,已知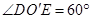 ,圆柱侧面积等于
,圆柱侧面积等于 .
.
(1)求圆柱的体积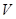 ;
;
(2)求异面直线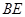 与
与 所成角
所成角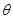 的大小.
的大小.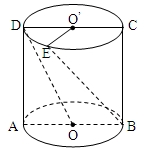
已知抛物线 .
.
(1)若直线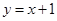 与抛物线
与抛物线 相交于
相交于 两点,求
两点,求 弦长;
弦长;
(2)已知△ 的三个顶点在抛物线
的三个顶点在抛物线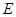 上运动.若点
上运动.若点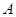 在坐标原点,
在坐标原点,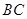 边过定点
边过定点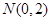 ,点
,点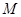 在
在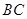 上且
上且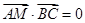 ,求点
,求点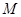 的轨迹方程.
的轨迹方程.