一条河的两岸有一段是平行的.在河的这一岸每相距5米在一棵树,在河的对岸每相距50米在一根电线杆.在这岸离开岸边25米处看对岸,看到对岸相邻的两根电线杆恰好被这岸的两棵树遮住,并且在这两棵树之间还有三棵树,求河宽.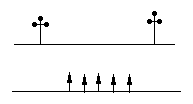
从广州某市,可乘坐普通列车或高铁,已知高铁的行驶路程是400千米,普通列车的行驶路程是高铁的行驶路程的1.3倍.
(1)求普通列车的行驶路程;
(2)若高铁的平均速度(千米/时)是普通列车平均速度(千米/时)的2.5倍,且乘坐高铁所需时间比乘坐普通列车所需时间缩短3小时,求高铁的平均速度.
如图,从A地到B地的公路需经过C地,图中AC=10千米,∠CAB=25°,∠CBA=37°.因城市规划的需要,将在A、B两地之间修建一条笔直的公路.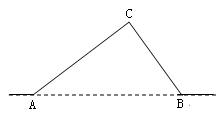
(1)求改直后的公路AB的长;
(2)问公路改直后该段路程比原来缩短了多少千米?(精确到0.1)
(sin25°≈0.42,cos25°≈0.91,sin37°≈0.60,tan37°≈0.75)
已知:如图,在平行四边形ABCD中,O为对角线BD的中点,过点O的直线EF分别交AD,BC于E,F两点,连结BE,DF.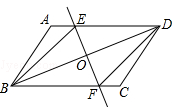
(1)求证:OE=OF.
(2)当∠DOE等于度时,四边形BFDE为菱形.(直接填写答案即可)
先化简,再求值: ,其中
,其中 .
.
如图1,在正方形ABCD中,E、F分别为BC、CD的中点,连接AE、BF,交点为G.
(1)求证:AE⊥BF;
(2)将 沿
沿 对折,得到
对折,得到 (如图2),延长
(如图2),延长 交
交 的延长线于点
的延长线于点 ,求
,求 的值;
的值;
(3)将 绕点
绕点 逆时针方向旋转,使边
逆时针方向旋转,使边 正好落在
正好落在 上,得到
上,得到 (如图3),若
(如图3),若 和
和 相交于点
相交于点 ,当正方形
,当正方形 的面积为4时,求四边形
的面积为4时,求四边形 的面积.
的面积.