如图,在平面直角坐标系中,A、B均在边长为1的正方形网格格点上.
(1)求线段AB所在直线的函数解析式,并写出当0≤y≤2时,自变量x的取值范围;
(2)将线段AB绕点B逆时针旋转90°,得到线段BC,请在下图中画出线段BC.若直线BC的函数解析式为y=kx+b,则y随x的增大而 __(填“增大”或“减小”).
甲、乙两人利用不同的交通工具,沿同一路线从 地出发前往 地,甲出发 后,乙出发,设甲与 地相距 ,乙与 地相距 ,甲离开 地的时间为 , 、 与 之间的函数图象如图所示.
(1)甲的速度是 ;
(2)当 时,求 关于 的函数解析式;
(3)当乙与 地相距 时,甲与 地相距 .

如图,在平面直角坐标系中,反比例函数 的图象上有一点 ,过点 作 轴于点 ,将点 向右平移2个单位长度得到点 ,过点 作 轴的平行线交反比例函数的图象于点 ,
(1)点 的横坐标为 (用含 的式子表示);
(2)求反比例函数的解析式.

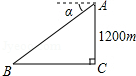
如图,某飞机于空中 处探测到目标 ,此时飞行高度 ,从飞机上看地平面指挥台 的俯角 ,求飞机 与指挥台 的距离(结果取整数)
(参考数据: , ,
某校学生会为了解环保知识的普及情况,从该校随机抽取部分学生,对他们进行了垃圾分类了解程度的调查,根调查收集的数据绘制了如下的扇形统计图,其中对垃圾分类非常了解的学生有30人
(1)本次抽取的学生有 人;
(2)请补全扇形统计图;
(3)请估计该校1600名学生中对垃圾分类不了解的人数.

图1,图2都是 的正方形网格,每个小正方形的顶点成为格点,每个小正方形的边长均为1,在每个正方形网格中标注了6个格点,这6个格点简称为标注点
(1)请在图1,图2中,以4个标注点为顶点,各画一个平行四边形(两个平行四边形不全等);
(2)图1中所画的平行四边形的面积为 .
