2008年5月12日,四川省汶川县发生8.0级大地震. 某校学生会倡导“抗震救灾,众志成城”自愿捐款活动并进行了抽样调查,得到了一组学生捐款情况的数据.下图是根据这组数据绘制的统计图,图中从左到右各长方形的高度之比为2:4:5:8:6.又知此次调查中捐款20元和25元的学生一共28人.
⑴他们一共调查了多少人?
⑵这组数据的众数、中位数是多少?
⑶若该校共有2000名学生,估计全校学生大约捐款多少元?
如图,抛物线 与 轴交于点 , ,与 轴交于点 ,已知 , 两点坐标分别是 , ,连接 , .
(1)求抛物线的表达式和 所在直线的表达式;
(2)将 沿 所在直线折叠,得到 ,点 的对应点 是否落在抛物线的对称轴上,若点 在对称轴上,请求出点 的坐标;若点 不在对称轴上,请说明理由;
(3)若点 是抛物线位于第三象限图象上的一动点,连接 交 于点 ,连接 , 的面积记为 , 的面积记为 ,求 的值最大时点 的坐标.

如图,在 中, , 是 的外接圆, 是直径,交 于点 ,点 在 上,连接 , 过点 作 交 的延长线于点 ,延长 交 于点 .
(1)求证: 是 的切线;
(2)若 , ,求 和 的长.

如图,过 点的直线 与 轴, 轴分别交于点 , 两点,且 ,过点 作 轴,垂足为点 ,交反比例函数 的图象于点 ,连接 , 的面积为6.
(1)求 值和点 的坐标;
(2)如图,连接 , ,点 在直线 上,且位于第二象限内,若 的面积是 面积的2倍,求点 的坐标.

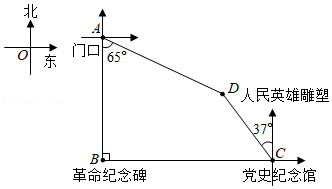
时代中学组织学生进行红色研学活动.学生到达爱国主义教育基地后,先从基地门口 处向正南方向走300米到达革命纪念碑 处,再从 处向正东方向走到党史纪念馆 处,然后从 处向北偏西 方向走200米到达人民英雄雕塑 处,最后从 处回到 处.已知人民英雄雕塑在基地门口的南偏东 方向,求革命纪念碑与党史纪念馆之间的距离(精确到1米).(参考数据: , , , , ,
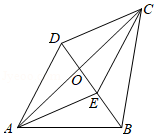
如图,在四边形 中, 与 相交于点 ,且 ,点 在 上,满足 .
(1)求证:四边形 是平行四边形;
(2)若 , , ,求四边形 的面积.