大润发超市进了一批成本为8元/个的文具盒。调查发现：这种文具盒每个星期
的销售量y（个）与它的定价x（元/个）的关系如图所示：
（1）求这种文具盒每个星期的销售量y（个）与它的定价x（元/个）之间的函数关系式（不必写出自变
量x的取值范围）；
（2）每个文具盒定价是多少元时，超市每星期销售这种文具盒（不考虑其他因素）可获得的利润最高？
最高利润是多少？
如图,在平面直角坐标系
中,⊙A与y轴相切于点
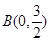,与x轴相交于M、N两点.如果点M的坐标为
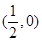,求点N的坐标.
如图,在△ABC中,∠ABC=2∠C,BD平分∠ABC,且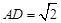
,
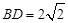,求AB的值.
已知抛物线与x轴相交于两点A(1,0),B(-3,0),与y轴相交于点C(0,3)．
(1)求此抛物线的函数表达式;
(2)如果点
是抛物线上的一点,求△ABD的面积．
如图,从热气球C处测得地面A、B两处的俯角分别为30°、45°,如果此时热气球C处的高度CD为100米,点A、D、B在同一直线上,求AB两处的距离.
现有三个自愿献血者,两人血型为O型,一人血型为A型.若在三人中随意挑选一人献血,两年以后又从此三人中随意挑选一人献血,试求两次所献血的血型均为O型的概率(要求：用列表或画树状图方法解答)