如图，在Rt△ABC中，∠ACB=90°，AC=8cm，BC=4cm，D、E分别为边AB、BC的中点，连结DE，点P从点A出发，沿折线AD－DE－EB运动，到点B停止．点P在AD上以
cm/s的速度运动，在折线DE－EB上以1cm/s的速度运动．当点P与点A不重合时，过点P作PQ⊥AC于点Q，以PQ为边作正方形PQMN，使点M落在线段AC上．设点P的运动时间为t(s).
（1）当点P在线段DE上运动时，线段DP的长为______cm,（用含t的代数式表示）．
（2）当点N落在AB边上时，求t的值．
（3）当正方形PQMN与△ABC重叠部分图形为五边形时，设五边形的面积为S（cm²），求S与t的函数关系式．
（4）连结CD．当点N于点D重合时，有一点H从点M出发，在线段MN上以2.5cm/s的速度沿M-N-M连续做往返运动，直至点P与点E重合时，点H停止往返运动；当点P在线段EB上运动时，点H始终在线段MN的中心处．直接写出在点P的整个运动过程中，点H落在线段CD上时t的取值范围．
如图1，在⊿ABC中，AB=BC,P为AB边上一点，连接CP，以PA,PC为邻边作平行四边形APCD,AC与PD相交于点E，已知∠ABC=∠AEP=
①.求证：∠EAP=∠EPA;
②.平行四边形APCD是否为矩形？请说明理由；
③.如图2，F为BC中点，连接FP,将∠AEP绕点E顺时针旋转适当的角度，得到∠MEN(点M,N分别是∠MEN的两边与BA,FP延长线的交点)，猜想线段EM与EN之间的数量关系，并证明你的结论。
如图，抛物线y＝－x2＋x＋3与x轴交于点A、B，与y轴交于点C，顶点为点D，对称轴l与直线BC交于点E，与x轴交于点F．
(1)求直线BC的解析式．
(2)设点P为该抛物线上的一个动点，以点P为圆心、r为半径作⊙P．
①当点P运动到点D时，若⊙P与直线BC相交，求r的取值范围；
②若r＝，是否存在点P使⊙P与直线BC相切？若存在，请求出点P的坐标；若不存在，请说明理由．
为了增强居民的节约用水意识，某市制定了新的水费收费标准：每户每月不超过5吨的部分，自来水公司按每吨2元收费；超过5吨部分，按每吨2.6元收费．设某用户月用水量为x吨，自来水公司应收水费y元．(1)试写出y(元)与x(吨)之间的函数关系式；
(2)该用户今年5月份的用水量为8吨，自来水公司应收水费多少元？
某市为了解九年级学生身体素质测试情况，随机抽取了本市九年级部分学生的身体素质测试成绩为样本，按A(优秀)、B(良好)、C(合格)、D(不合格)四个等级进行统计，并将统计结果绘制成如下统计图表．请你结合图表中所给信息解答下列问题：
(1)请将上面表格中缺少的数据补充完整；
(2)扇形统计图中“A”部分所对应的圆心角的度数是；
(3)该市九年级共有80 000名学生参加了身体素质测试，试估计测试成绩合格以上(含合格)的人数．
如图，将矩形纸片ABCD沿EF折叠，使A点与C点重合，点D落在点G处，EF为折痕．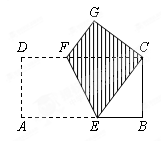
(1)求证：△FGC≌△EBC；
(2)若AB＝8，AD＝4，求四边形ECGF(阴影部分)的面积．（7分