某校为实施国家“营养早餐”工程,食堂用甲、乙两种原料配制成某种营养食品,已知这两种原料的维生素C含量及购买这两种原料的价格如下表: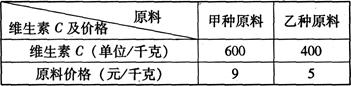
现要配制这种营养食品20千克,要求每千克至少含有480单位的维生素C.设购买甲种原料x千克.
(1)至少需要购买甲种原料多少千克?
(2)设食堂用于购买这两种原料的总费用为y元,求y与x的函数关系式.并说明购买甲种原料多少千克时,总费用最少?
为了继承和发扬延安精神,满足青少年热爱红色革命根据地,了解延安革命历程的愿望,相关部门在当地中小学选拔了一批优秀共青团员和少先队员,组织他们利用节假日,在红色革命旧址(纪念馆)做“小小讲解员”,每位“小小讲解员”都要通过抽签的方式确定各自的讲解地点.讲解地点有: .枣园革命旧址, .杨家岭革命旧址, .延安革命纪念馆, .鲁艺学院旧址.抽签规则如下:
将正面分别写有字母 、 、 、 的四张卡片(除了正面字母不同外,其余均相同)背面朝上,洗匀,先由一位“小小讲解员”随机抽取一张卡片,这张卡片上的字母表示的讲解地点,即为他抽取的讲解地点,然后将卡片放回,洗匀,再由下一位“小小讲解员”抽取.已知小明和小亮都是“小小讲解员”.
(1)求小明抽到的讲解地点是“ .枣园革命旧址”的概率;
(2)请用列表或画树状图的方法,求小明与小亮抽到同一讲解地点的概率.
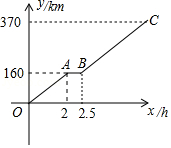
一天,小华爸爸开车带全家到西安游玩,实现爷爷奶奶想看大雁塔,游大唐芙蓉园的愿望,由导航可知,从小华家到西安大雁塔的路程为 ,他们全家早上 从家出发,途中他们在一个服务区短暂休息之后,继续行驶,在上午 时,他们距离西安大雁塔还有 ,如图是他们从家到西安大雁塔的过程中,行驶路程 与所用时间 之间的函数图象,请根据相关信息,解答下列问题:
(1)求小华一家在服务区休息了多长时间?
(2)求 所在直线的函数表达式,并求小华一家这天几点到达西安大雁塔?
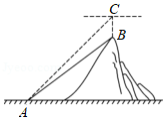
如图所示,某集团的项目组计划在山脚下 点与山顶 点之间修建一条索道,现利用无人机测算 、 两点间的距离.无人机飞至山顶点 的正上方点 处时,测得山脚下 点的俯角约为 , 点与 点的高度差为 , ,求山脚下 点到山顶 点的距离 .
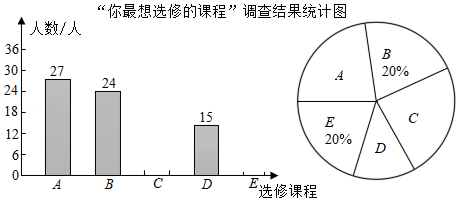
为了丰富学生的课余生活,满足学生个性化发展需求,某校计划在七年级开设选修课为了解学生选课情况,科学合理的配制资源,校教务处随机抽取了若干名七年级学生,对“你最想选修的课程”进行调查,可选修的课程有: (书法)、 (航模)、 (演讲与主持)、 (足球)、 (文学创作).经统计,被调查学生按学校的要求,并结合自己的喜好,每人都从这五门课程中选择了一门选修课.现将调查结果绘制成如图两幅不完整的统计图.
请根据以上提供的信息,解答下列问题:
(1)在这次调查中,课程 (演讲与主持)的选修人数为 ,课程 (文学创作)的选修人数为 ;
(2)在这次调查中,哪门课程的选修人数少于各门课程选修人数的平均数?
(3)若该校七年级有900名学生,请估计该年级想选修课程 (航模)的学生人数.
如图,在 中, , 是边 的中点,延长 到点 ,使 ,延长 到点 ,使 ,连接 , ,求证: .