如图,在△ABC中,∠BAC=30°,以AB为直径的⊙O经过点C.过点C作⊙O的切线交AB的延长线于点P.点D为圆上一点,且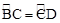 ,弦AD的延长线交切线PC于点E,连接BC.
,弦AD的延长线交切线PC于点E,连接BC.
(1)判断OB和BP的数量关系,并说明理由;
(2)若⊙O的半径为2,求AE的长.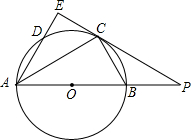
2011年5月9日至14日,德州市共有35000余名学生参加中考体育测试,为了了解九年级男生立定跳远的成绩,从某校随机抽取了50名男生的测试成绩,根据测试评分标准,将他们的得分按优秀、良好、及格、不及格(分别用A、B、C、D表示)四个等级进行统计,并绘制成下面的扇形图和统计表:
| 等级 |
成绩 |
频数(人数) |
频率 |
| A |
90~100 |
19 |
0.38 |
| B |
75~89 |
m |
x |
| C |
60~74 |
n |
y |
| D |
60以下 |
3 |
0.06 |
| 合计 |
50 |
1.00 |
请你根据以上图表提供的信息,解答下列问题:
(1)m= ,n= ,x= ,y= ;
(2)在扇形图中,C等级所对应的圆心角是 度;
(3)如果该校九年级共有500名男生参加了立定跳远测试,那么请你估计这些男生成绩等级达到优秀和良好的共有多少人?
解不等式组,并把解集在数轴上表示出来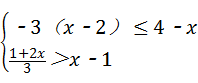 .
.
如图,某广场设计的一建筑物造型的纵截面是抛物线的一部分,抛物线的顶点O落在水平面上,对称轴是水平线OC.点A、B在抛物线造型上,且点A到水平面的距离AC=4米,点B到水平面距离为2米,OC=8米.
(1)请建立适当的直角坐标系,求抛物线的函数解析式;
(2)为了安全美观,现需在水平线OC上找一点P,用质地、规格已确定的圆形钢管制作两根支柱PA、PB对抛物线造型进行支撑加固,那么怎样才能找到两根支柱用料最省(支柱与地面、造型对接方式的用料多少问题暂不考虑)时的点P?(无需证明)
(3)为了施工方便,现需计算出点O、P之间的距离,那么两根支柱用料最省时点O、P之间的距离是多少?(请写出求解过程)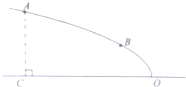
如图,在
中,点
是
边上(端点除外)的一个动点,过点
作直线
.设
交
的平分线于点
 ,交
的外角平分线于点
,连接
、
.那么当点
运动到何处时,四边形
是矩形?并证明你的结论.
,交
的外角平分线于点
,连接
、
.那么当点
运动到何处时,四边形
是矩形?并证明你的结论.

根据给出的下列两种情况,请用直尺和圆规找到一条直线,把△ABC恰好分割成两个等腰三角形(不写做法,但需保留作图痕迹);并根据每种情况分别猜想:∠A与∠B有怎样的数量关系时才能完成以上作图?并举例验证猜想所得结论.
(1)如图①△ABC中,∠C=90°,∠A=24°
①作图:
②猜想:
③验证:
(2)如图②△ABC中,∠C=84°,∠A=24°.
①作图:
②猜想:
③验证: