如图,在平行四边形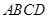 中,边
中,边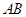 所在直线的方程为
所在直线的方程为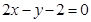 ,点
,点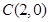 .
.
(1)求直线 的方程;
的方程;
(2)求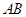 边上的高
边上的高 所在直线的方程.
所在直线的方程.
在△ 中,角
中,角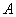 、
、 、
、 所对的边分别为
所对的边分别为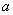 、
、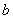 、
、 ,且
,且 .
.
(Ⅰ)若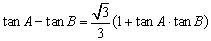 ,求角
,求角 ;
;
(Ⅱ)设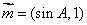 ,
, ,试求
,试求 的最大值.
的最大值.
已知不等式 的解集为A,函数
的解集为A,函数 的定义域为B.
的定义域为B.
(Ⅰ)若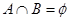 ,求
,求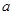 的取值范围;
的取值范围;
(Ⅱ)证明:函数 的图象关于原点对称。
的图象关于原点对称。
如图,点A,B是单位圆上的两点,A,B点分别在第一、二象限,点C是圆与x轴正半轴的交点,△AOB是正三角形,若点A的坐标为( ,
,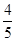 ),记∠COA=α.
),记∠COA=α.
(1)求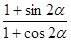 的值;
的值;
(2)求|BC|2的值.
已知 为坐标原点,
为坐标原点, ,
, (
( ,
, 是常数),若
是常数),若
(1)求 关于
关于 的函数关系式
的函数关系式 ;
;
(2)若 的最大值为
的最大值为 ,求
,求 的值;
的值;
(3)利用(2)的结论,用“五点法”作出函数 在长度为一个周期的闭区间上的简图,并指出其单调区间。
在长度为一个周期的闭区间上的简图,并指出其单调区间。
已知向量 ,
, ,
,
(1)求证: ⊥
⊥ ;(2)
;(2) ,求
,求 的值
的值