如图,点A,B是单位圆上的两点,A,B点分别在第一、二象限,点C是圆与x轴正半轴的交点,△AOB是正三角形,若点A的坐标为( ,
,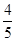 ),记∠COA=α.
),记∠COA=α.
(1)求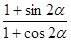 的值;
的值;
(2)求|BC|2的值.
(本小题满分13分)已知实数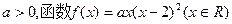 有极大值32.
有极大值32.
(1)求函数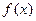 的单调区间;(2)求实数
的单调区间;(2)求实数 的值.
的值.
(本小题满分13分)已知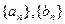 均为等差数列,且
均为等差数列,且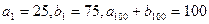 ,求数列
,求数列 的前100项之和。
的前100项之和。
(本小题满分14分) 已知函数 在
在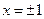 处取得极值。
处取得极值。
(Ⅰ)求函数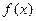 的解析式;
的解析式;
(Ⅱ)求证:对于区间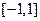 上任意两个自变量的值
上任意两个自变量的值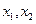 ,都有
,都有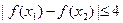 ;
;
(Ⅲ)若过点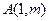 可作曲线
可作曲线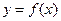 的
的 三条切线,求实数
三条切线,求实数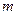 的取值范围。
的取值范围。
(本小题满分13分)已知函数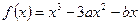 ,其中
,其中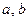 为实数.
为实数.
(Ⅰ) 若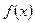 在
在 处取得的极值为
处取得的极值为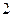 ,求
,求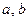 的值;
的值;
(Ⅱ)若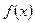 在区间
在区间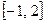 上为减函数,且
上为减函数,且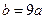 ,求
,求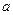 的取值范围.
的取值范围.
(本小题满分12分) 某租赁公司拥有汽车100辆.当每辆车的月租金为3000元时,可全 部租出.当每辆车的月租金每增加50元时,未租出的车将会增加一辆.租出的车每辆每月需要维护费150元,未租出的车每辆每月需要维护费50元.
部租出.当每辆车的月租金每增加50元时,未租出的车将会增加一辆.租出的车每辆每月需要维护费150元,未租出的车每辆每月需要维护费50元.
(1)当每辆车的月租金定为3600元时,能租出多少辆车?
(2)当每辆车的月租金定为多少元时,租赁公司的月收益最大?最大月收益是多少?