直线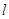 与椭圆
与椭圆 交于
交于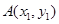 ,
,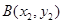 两点,已知
两点,已知
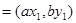 ,
,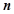
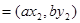 ,若
,若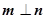 且椭圆的离心率
且椭圆的离心率 ,又椭圆经过点
,又椭圆经过点 ,
,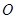 为坐标原点.
为坐标原点.
(Ⅰ)求椭圆的方程;
(Ⅱ)若直线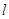 过椭圆的焦点
过椭圆的焦点 (
(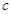 为半焦距),求直线
为半焦距),求直线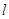 的斜率
的斜率 的值;
的值;
(Ⅲ)试问: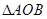 的面积是否为定值?如果是,请给予证明;如果不是,请说明理由.
的面积是否为定值?如果是,请给予证明;如果不是,请说明理由.
若直线l: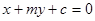 与抛物线
与抛物线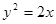 交于A、B两点,O点是坐标原点。
交于A、B两点,O点是坐标原点。
(1)当m=-1,c=-2时,求证:OA⊥OB;
(2)若OA⊥OB,求证:直线l恒过定点;并求出这个定点坐标。
(3)当OA⊥OB时,试问△OAB的外接圆与抛物线的准线位置关系如何?证明你的结论。
已知命题p:方程 表示焦点在y轴上的椭圆;命题q:双曲线
表示焦点在y轴上的椭圆;命题q:双曲线 的离心率
的离心率 ;若“
;若“ ”为真,“
”为真,“ ”为假,求实数
”为假,求实数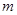 的取值范围.
的取值范围.
已知圆C:
(1)若不过原点的直线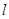 与圆C相切,且在
与圆C相切,且在 轴、
轴、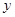 轴上的截距相等,求直线
轴上的截距相等,求直线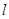 的方程;
的方程;
(2)从圆C外一点 向圆引一条切线,切点为M,O为坐标原点,且有
向圆引一条切线,切点为M,O为坐标原点,且有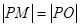 ,求点P的轨迹方程.
,求点P的轨迹方程.
已知偶函数 ,对任意
,对任意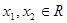 ,恒有
,恒有 ,求:(1)
,求:(1)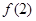 的值;(2)
的值;(2) 的表达式;
的表达式;
(3)对任意的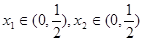 ,都有
,都有 成立时,求
成立时,求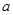 的取值范围.
的取值范围.
在某次测验中,有6位同学的平均成绩为75分,用 表示编号为
表示编号为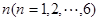 的同学所得成绩,且前5位同学的成绩如下:
的同学所得成绩,且前5位同学的成绩如下:
编号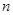 |
1 |
2 |
3 |
4 |
5 |
成绩 |
70 |
76 |
72 |
70 |
72 |
(1)求第6位同学的成绩 ,及这6位同学成绩的标准差
,及这6位同学成绩的标准差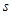 ;
;
(2)从前5位同学中,随机地选2位同学,求恰有1位同学的成绩在区间(68,75)中的概率.