如图,CD是线段AB上任意两点,E是线段AC的中点,F是线段BD的中点,若EF=a,CD=b,求AB的长.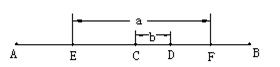
某地有两家通讯公司,移动通讯收费标准如下:
第一家规定不收月租费,每分钟收费是0.6元;
第二家规定要收月租费,每月收50元,另外每分钟收费0.4元[(1)某用户每月打电话的时间为x分钟,请你写出这两种收费方式下应该支付的费用;
(2)某用户每月打电话的时间为200分钟,你认为应该采用哪一家通讯公司合算;
(3)你认为每月打电话时间超过多少分钟,第二家通讯公司比较合算
直线AB、CD相交于点O,OE平分∠AOD,∠FOC=90°,∠1=40°,求∠2与∠3的度数。
如图B、C两点把线段AD分成2:3:4三部分,M是AD的中点,CD=8,求MC的长。
.化简求值 ,其中
,其中