一缉私艇A发现在北偏东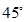 方向,距离12 nmile的海面上有一走私船C正以10 nmile/h的速度沿东偏南
方向,距离12 nmile的海面上有一走私船C正以10 nmile/h的速度沿东偏南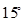 方向逃窜.缉私艇的速度为14 nmile/h, 若要在最短的时间内追上该走私船,缉私艇应沿北偏东
方向逃窜.缉私艇的速度为14 nmile/h, 若要在最短的时间内追上该走私船,缉私艇应沿北偏东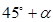 的方向去追,.求追及所需的时间和
的方向去追,.求追及所需的时间和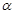 角的正弦值.
角的正弦值.
在平面直角坐标系 ,已知圆心在第二象限、半径为
,已知圆心在第二象限、半径为 的圆C与直线y=x相切于
的圆C与直线y=x相切于
坐标原点O.椭圆 与圆C的一个交点到椭圆两焦点的距离之和为
与圆C的一个交点到椭圆两焦点的距离之和为 .
.
(1)求圆C的方程;
(2)圆C上是否存在异于原点的点Q,使 (F为椭圆右焦点),若存在,请
(F为椭圆右焦点),若存在,请
求出点Q的坐标;若不存在,请说明理由.
设平面向量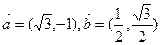 ,若存在实数
,若存在实数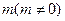 和角
和角 ,其中
,其中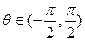 ,使向量
,使向量 ,且
,且 .
.
(1).求 的关系式;
的关系式;
(2).若 ,求
,求 的最小值,并求出此时的
的最小值,并求出此时的 值.
值.
观察下列三角形数表
1 -----------第一行
2 2 -----------第二行
3 4 3 -----------第三行
4 7 7 4 -----------第四行
5 11 14 11 5
…… … …
…… … ……
假设第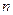 行的第二个数为
行的第二个数为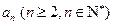 ,
,
(Ⅰ)依次写出第六行的所有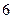 个数字;
个数字;
(Ⅱ)归纳出 的关系式并求出
的关系式并求出 的通项公式;
的通项公式;
(Ⅲ)设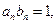 求证:
求证: …
…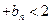
如图,在组合体中,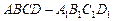 是一个长方体,
是一个长方体, 是一个四棱锥.
是一个四棱锥.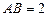 ,
,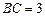 ,点
,点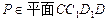 且
且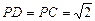 .
.
(Ⅰ)证明: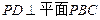 ;
;
(Ⅱ)若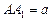 ,当
,当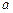 为何值时,
为何值时, .
.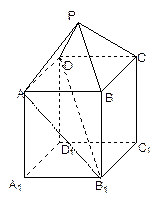
已知函数f(x)= 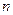 +lnx的图像在点P(m,f(m))处的切线方程为y="x" ,
+lnx的图像在点P(m,f(m))处的切线方程为y="x" ,
设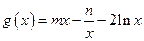 .
.
(1)求证:当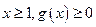 恒成立;
恒成立;
(2)试讨论关于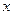 的方程:
的方程: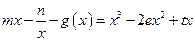 根的个数.
根的个数.