(本小题满分13分)某同学大学毕业后在一家公司上班,工作年限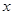 和年收入
和年收入 (万元),有以下的统计数据:
(万元),有以下的统计数据:
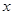 |
3 |
4 |
5 |
6 |
 |
2.5 |
3 |
4 |
4.5 |
(Ⅰ)请画出上表数据的散点图;
(Ⅱ)请根据上表提供的数据,用最小二乘法求出 关于
关于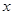 的线性回归方程
的线性回归方程 ;
;
(Ⅲ)请你估计该同学第8年的年收入约是多少?
(参考公式: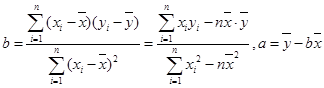 )
)
(本小题满分13分)已知椭圆 :
: (
(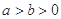 )的右焦点为
)的右焦点为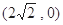 ,且椭圆
,且椭圆 上一点
上一点 到其两焦点
到其两焦点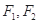 的距离之和为
的距离之和为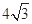 .
.
(Ⅰ)求椭圆 的标准方程;
的标准方程;
(Ⅱ)设直线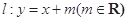 与椭圆
与椭圆 交于不同两点
交于不同两点 ,
, ,且
,且 .若点
.若点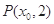 满足
满足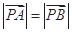 ,求
,求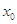 的值.
的值.
(本小题满分12分)某大型企业一天中不同时刻的用电量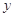 (单位:万千瓦时)关于时间
(单位:万千瓦时)关于时间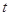 (
(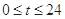 ,单位:小时)的函数
,单位:小时)的函数 近似地满足
近似地满足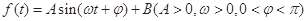 ,下图是该企业一天中在0点至12点时间段用电量
,下图是该企业一天中在0点至12点时间段用电量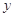 与时间
与时间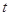 的大致图象.
的大致图象.
(Ⅰ)根据图象,求 ,
,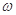 ,
, ,
, 的值;
的值;
(Ⅱ)若某日的供电量 (万千瓦时)与时间
(万千瓦时)与时间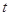 (小时)近似满足函数关系式
(小时)近似满足函数关系式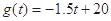 (
( ).当该日内供电量小于该企业的用电量时,企业就必须停产.请用二分法计算该企业当日停产的大致时刻(精确度0.1).
).当该日内供电量小于该企业的用电量时,企业就必须停产.请用二分法计算该企业当日停产的大致时刻(精确度0.1).
参考数据:
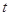 (时) (时) |
10 |
11 |
12 |
11.5 |
11.25 |
11.75 |
11.625 |
11.6875 |
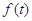 (万千瓦时) (万千瓦时) |
2.25 |
2.433 |
2.5 |
2.48 |
2.462 |
2.496 |
2.490 |
2.493 |
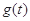 (万千瓦时) (万千瓦时) |
5 |
3.5 |
2 |
2.75 |
3. 125 |
2.375 |
2.563 |
2.469 |
(本小题满分12分)已知数列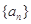 的前
的前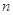 项和为
项和为 ,且
,且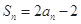 ;数列
;数列 满足
满足 ,
,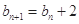 .
. .
.
(Ⅰ)求数列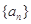 ,
, 的通项公式;
的通项公式;
(Ⅱ)记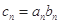 ,
, .求数列
.求数列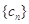 的前
的前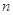 项和
项和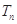 .
.
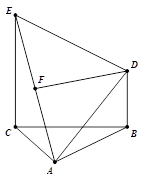
(本小题满分12分)如图,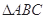 为正三角形,
为正三角形,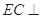 平面
平面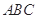 ,
,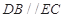 ,
,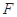 为
为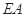 的中点,
的中点,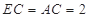 ,
,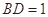 .
.
(Ⅰ)求证: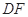
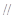 平面
平面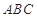 ;
;
(Ⅱ)求平面 与平面
与平面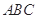 所成的锐二面角的余弦值.
所成的锐二面角的余弦值.
(本小题满分12分)口袋中装有除颜色,编号不同外,其余完全相同的2个红球,4个黑球.现从中同时取出3个球.
(Ⅰ)求恰有一个黑球的概率;
(Ⅱ)记取出红球的个数为随机变量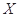 ,求
,求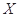 的分布列和数学期望
的分布列和数学期望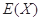 .
.