(本小题满分12分)
某出版社新出版一本高考复习用书,该书的成本为 元一本,经销过程中每本书需付给代理商
元一本,经销过程中每本书需付给代理商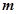 元
元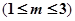 的劳务费,经出版社研究决定,新书投放市场后定价为
的劳务费,经出版社研究决定,新书投放市场后定价为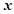 元一本,
元一本,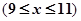 ,预计一年的销售量为
,预计一年的销售量为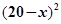 万本.
万本.
(Ⅰ)求该出版社一年的利润 (万元)与每本书的定价
(万元)与每本书的定价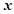 的函数关系式;
的函数关系式;
(Ⅱ)若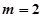 时,当每本书的定价为多少元时,该出版社一年利润
时,当每本书的定价为多少元时,该出版社一年利润 最大,并求出
最大,并求出 的最大值.
的最大值.
已知椭圆C的中心在原点,焦点F在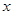 轴上,离心率
轴上,离心率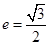 ,点
,点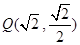 在椭圆C上.
在椭圆C上.
(1)求椭圆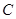 的标准方程;
的标准方程;
(2)若斜率为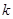
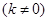 的直线
的直线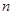 交椭圆
交椭圆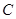 与
与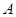 、
、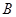 两点,且
两点,且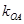 、
、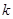 、
、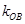 成等差数列,点M(1,1),求
成等差数列,点M(1,1),求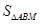 的最大值.
的最大值.
如图,平面 平面
平面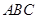 ,
, 是等腰直角三角形,
是等腰直角三角形,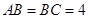 ,四边形
,四边形 是直角梯形,
是直角梯形,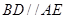 ,
,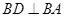 ,
, ,点
,点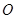 、
、 分别为
分别为 、
、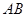 的中点.
的中点.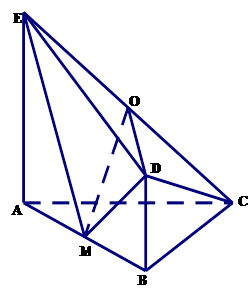
(1)求证: 平面
平面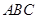 ;
;
(2)求直线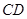 和平面
和平面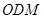 所成角的正弦值;
所成角的正弦值;
(3)能否在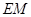 上找到一点
上找到一点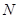 ,使得
,使得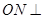 平面
平面 ?若能,请指出点
?若能,请指出点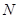 的位置,并加以证明;若不能,请说明理由.
的位置,并加以证明;若不能,请说明理由.
已知数列 各项为非负实数,前n项和为
各项为非负实数,前n项和为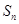 ,且
,且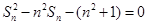
(1)求数列 的通项公式;
的通项公式;
(2)当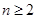 时,求
时,求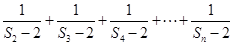 .
.
如图,从 到
到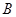 有6条网线,数字表示该网线单位时间内可以通过的最大信息量,现从中任取3条网线且使每条网线通过最大信息量,设这三条网线通过的最大信息之和为
有6条网线,数字表示该网线单位时间内可以通过的最大信息量,现从中任取3条网线且使每条网线通过最大信息量,设这三条网线通过的最大信息之和为 .
.
(1)当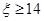 时,线路信息畅通,求线路信息畅通的概率;
时,线路信息畅通,求线路信息畅通的概率;
(2)求 的分布列和数学期望.
的分布列和数学期望.
已知函数 的最大值为2.
的最大值为2.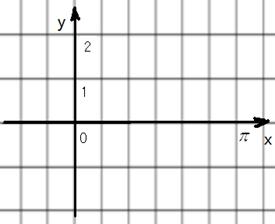
(1)求 的值及
的值及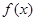 的最小正周期;
的最小正周期;
(2)在坐标纸上做出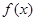 在
在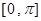 上的图像.
上的图像.