(本小题满分15分)已知 .
.
(1)如果函数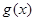 的单调递减区间为
的单调递减区间为 ,求函数
,求函数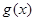 的解析式;
的解析式;
(2)在(Ⅰ)的条件下,求函数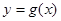 的图像在点
的图像在点 处的切线方程;
处的切线方程;
(3)若不等式 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
如图,已知锐角△ABC的面积为1,正方形DEFG是△ABC的一个内接三角形,
DG∥BC,求正方形DEFG面积的最大值.
已知过抛物线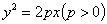 的焦点,斜率为
的焦点,斜率为 的直线交抛物线于
的直线交抛物线于
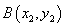 (
( )两点,且
)两点,且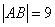 .
.
(1)求该抛物线的方程;
(2) 为坐标原点,
为坐标原点,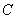 为抛物线上一点,若
为抛物线上一点,若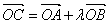 ,求
,求 的值.
的值.
已知函数 。
。
(1)求m的值;
(2)判断 上的单调性并加以证明;
上的单调性并加以证明;
(3)当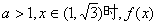 的值域是(1,+
的值域是(1,+ ),求a的值。
),求a的值。
如图,四棱锥E—ABCD中,ABCD是矩形,平面EAB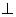 平面ABCD,AE=EB=BC=2,F为CE上的点,且BF
平面ABCD,AE=EB=BC=2,F为CE上的点,且BF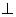 平面AC E.
平面AC E.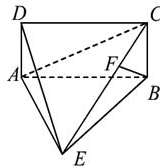
(1)求证:AE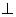 BE;
BE;
(2)求三棱锥D—AEC的体积;
(3)求二面角A—CD—E的余弦值.
已知数列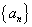 ,首项a 1 =3且2a n+1="S" n・S n-1 (n≥2).
,首项a 1 =3且2a n+1="S" n・S n-1 (n≥2).
(1)求证:{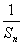 }是等差数列,并求公差;
}是等差数列,并求公差;
(2)求{a n }的通项公式;
(3)数列{an }中是否存在自然数k0,使得当自然数k≥k 0时使不等式a k>a k+1对任意大于等于k的自然数都成立,若存在求出最小的k值,否则请说明理由.