已知数列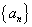 ,首项a 1 =3且2a n+1="S" n・S n-1 (n≥2).
,首项a 1 =3且2a n+1="S" n・S n-1 (n≥2).
(1)求证:{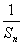 }是等差数列,并求公差;
}是等差数列,并求公差;
(2)求{a n }的通项公式;
(3)数列{an }中是否存在自然数k0,使得当自然数k≥k 0时使不等式a k>a k+1对任意大于等于k的自然数都成立,若存在求出最小的k值,否则请说明理由.
如图,直线AB过圆心O,交 于F(不与B重合),直线
于F(不与B重合),直线 与
与 相切于C,交AB于E,且与AF垂直,垂足为G,连结AC.
相切于C,交AB于E,且与AF垂直,垂足为G,连结AC.
求证:(1) ;(2)
;(2) .
.
已知函数 .
.
(1)当 时,求
时,求 的极值;
的极值;
(2)当 时,讨论
时,讨论 的单调性;
的单调性;
(3)若对任意的 ,
, ,恒有
,恒有 成立,求实数
成立,求实数 的取值范围.
的取值范围.
已知圆 ,直线
,直线 与圆
与圆 相切,且交椭圆
相切,且交椭圆 于
于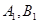 两点,c是椭圆的半焦距,
两点,c是椭圆的半焦距, .
.
(1)求m的值;
(2)O为坐标原点,若 ,求椭圆
,求椭圆 的方程;
的方程;
(3)在(2)的条件下,设椭圆 的左右顶点分别为A,B,动点
的左右顶点分别为A,B,动点 ,直线
,直线 与直线
与直线 分别交于M,N两点,求线段MN的长度的最小值.
分别交于M,N两点,求线段MN的长度的最小值.
如图所示,ABCD是正方形,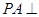 平面ABCD,E,F是AC,PC的中点.
平面ABCD,E,F是AC,PC的中点.
(1)求证: ;
;
(2)若 ,求三棱锥
,求三棱锥 的体积.
的体积.
某单位N名员工参加“社区低碳你我他”活动,他们的年龄在25岁至50岁之间,按年龄分组:第1组 ,第2组
,第2组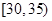 ,第3组
,第3组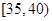 ,第4组
,第4组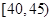 ,第5组
,第5组 ,得到的频率分布直方图如图所示,下表是年龄的频率分布表.
,得到的频率分布直方图如图所示,下表是年龄的频率分布表.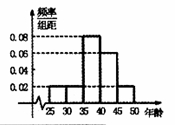

(1)求正整数 的值;
的值;
(2)现要从年龄较小的第1,2,3组中用分层抽样的方法抽取6人,则年龄在第1,2,3组的人数分别是多少?
(3)在(2)的条件下,从这6人中随机抽取2人参加社区宣传交流活动,求恰有1人在第3组的概率.