如图所示,机器人海宝按照以下程序运行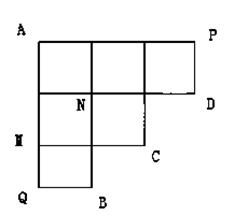
1从A出发到达点B或C或D，到达点B、C、D之一就停止；
②每次只向右或向下按路线运行；
③在每个路口向下的概率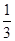
；
④到达P时只向下，到达Q点只向右．
（1）求海宝过点从A经过M到点B的概率，求海宝过点从A经过N到点C的概率；
（2）记海宝到点B、C、D的事件分别记为X=1，X=2，X=3，求随机变量X的分布列及期望．
已知定义域为R的函数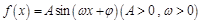
的一段图象如图所示．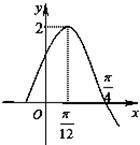
（1）求
的解析式；
（2）若
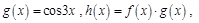求函数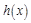
的单调递增区间．
设数列
的各项均为正实数，
，若数列
满足
，
，其中
为正常数，且
.
（1）求数列的通项公式；
（2）是否存在正整数
，使得当
时，
恒成立？若存在，求出使结论成立的的取值范围和相应的的最小值；若不存在，请说明理由；
（3）若
，设数列
对任意的
，都有
成立，问数列是不是等比数列？若是，请求出其通项公式；若不是，请说明理由.
若函数
（
为实常数）.
（1）当
时，求函数
在
处的切线方程；
（2）设
.
①求函数
的单调区间；
②若函数
的定义域为
，求函数
的最小值
.
某地开发了一个旅游景点，第1年的游客约为100万人，第2年的游客约为120万人.某数学兴趣小组综合各种因素预测：①该景点每年的游客人数会逐年增加；②该景点每年的游客都达不到130万人.该兴趣小组想找一个函数
来拟合该景点对外开放的第
年与当年的游客人数
（单位：万人）之间的关系.
（1）根据上述两点预测，请用数学语言描述函数所具有的性质；
（2）若
=
，试确定
的值，并考察该函数是否符合上述两点预测；
（3）若=
，欲使得该函数符合上述两点预测，试确定
的取值范围．
，
，
为等边三角形，且平面
平面ABE，
，P为CE中点．
；