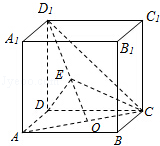
(本小题满分12分)已知正方体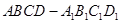 的棱长为2,
的棱长为2,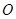 是AC的中点,E是线段
是AC的中点,E是线段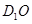 上一点,且
上一点,且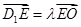 .
.
(1)求证: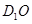 ⊥AC;
⊥AC;
(2)若DE⊥平面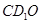 ,求
,求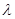 的值,并求三棱锥C-DEO的体积.
的值,并求三棱锥C-DEO的体积.
(本小题满分12分)某班50位学生2015届中考试数学成绩的频率直方分布图如图所示,其中成绩分组区间是:[40,50),[50,60),[60,70),[70,80),[80,90),[90,100].
(1)求图中x的值;
(2)从成绩在[50,70)的学生中随机选取2人,求这2人成绩都在[60,70)中的概率.
(本小题满分12分)如图所示,在四边形ABCD中,∠D=2∠B,且AD=1,CD=3,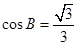 .
.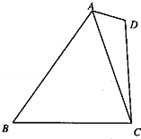
(1)求△ACD的面积;
(2)若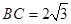 ,求AB的长.
,求AB的长.
(本小题满分14分)已知数列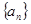 中,
中,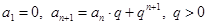 ,
,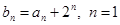 ,2,3,…
,2,3,…
(Ⅰ)求证数列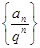 是等差数列;
是等差数列;
(Ⅱ)试比较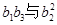 的大小;
的大小;
(Ⅲ)求正整数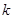 ,使得对于任意的正整数
,使得对于任意的正整数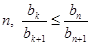 恒成立.
恒成立.
(本小题满分14分)设函数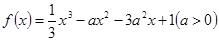 .
.
(Ⅰ)求函数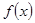 的单调区间、极大值和极小值.
的单调区间、极大值和极小值.
(Ⅱ)若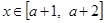 时,恒有
时,恒有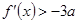 ,求实数
,求实数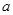 的取值范围.
的取值范围.