如图,平面上有四个点A、B、C、D,根据下列语句画图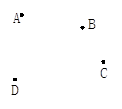
(1)画直线AB、CD交于E点;
(2)画线段AC、BD交于点F;
(3)连接E、F交BC于点G;
(4)连接AD,并将其反向延长;
(5)作射线BC;
(6)取一点P,使P在直线AB上又在直线CD上.
(2014年吉林省10分)如图①,直线l:y=mx+n(m>0,n<0)与x,y轴分别相交于A,B两点,将△AOB绕点O逆时针旋转90°,得到△COD,过点A,B,D的抛物线P叫做l的关联抛物线,而l叫做P的关联直线.
(1)若l:y=﹣2x+2,则P表示的函数解析式为 ;若P:y=﹣x2﹣3x+4,则l表示的函数解析式为 .
(2)求P的对称轴(用含m,n的代数式表示);
(3)如图②,若l:y=﹣2x+4,P的对称轴与CD相交于点E,点F在l上,点Q在P的对称轴上.当以点C,E,Q,F为顶点的四边形是以CE为一边的平行四边形时,求点Q的坐标;
(4)如图③,若l:y=mx﹣4m,G为AB中点,H为CD中点,连接GH,M为GH中点,连接OM.若OM=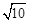 ,直接写出l,P表示的函数解析式.
,直接写出l,P表示的函数解析式.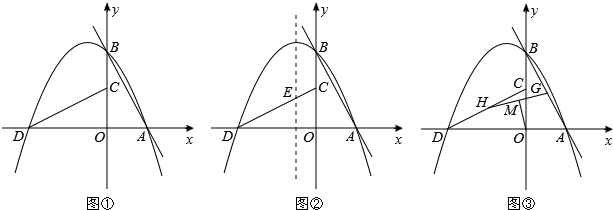
(2014年湖南岳阳10分)数学活动﹣求重叠部分的面积
(1)问题情境:如图①,将顶角为120°的等腰三角形纸片(纸片足够大)的顶点P与等边△ABC的内心O重合,已知OA=2,则图中重叠部分△PAB的面积为 .
(2)探究1:在(1)的条件下,将纸片绕P点旋转至如图②所示位置,纸片两边分别与AC,AB交于点E,F,图②中重叠部分的面积与图①重叠部分的面积是否相等?如果相等,请给予证明;如果不相等,请说明理由.
(3)探究2:如图③,若∠CAB=α(0°<α<90°),AD为∠CAB的角平分线,点P在射线AD上,且AP=2,以P为顶点的等腰三角形纸片(纸片足够大)与∠CAB的两边AC,AB分别交于点E、F,∠EPF=180°﹣α,求重叠部分的面积.(用α或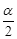 的三角函数值表示)
的三角函数值表示)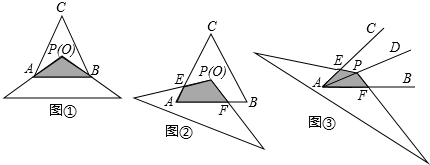
(年湖北黄冈13分)如图,在四边形OABC中,AB∥OC,BC⊥x轴于C, ,动点P从O点出发,沿x轴正方向以2个单位/秒的速度运动.过P作PQ⊥OA于Q.设P点运动的时间为t秒(0 < t < 2),ΔOPQ与四边形OABC重叠的面积为S.
,动点P从O点出发,沿x轴正方向以2个单位/秒的速度运动.过P作PQ⊥OA于Q.设P点运动的时间为t秒(0 < t < 2),ΔOPQ与四边形OABC重叠的面积为S.
(1)求经过O、A、B三点的抛物线的解析式并确定顶点M的坐标;
(2)用含t的代数式表示P、Q两点的坐标;
(3)将ΔOPQ绕P点逆时针旋转90°,是否存在t,使得ΔOPQ的顶点O或Q落在抛物线上?若存在,直接写出t的值;若不存在,请说明理由;
(4)求S与t的函数解析式.
(年湖北江汉油田、潜江、天门、仙桃10分)如图①,△ABC与△DEF是将△ACF沿过A点的某条直线剪开得到的(AB,DE是同一条剪切线).平移△DEF使顶点E与AC的中点重合,再绕点E旋转△DEF,使ED,EF分别与AB,BC交于M,N两点.
(1)如图②,△ABC中,若AB=BC,且∠ABC=90°,则线段EM与EN有何数量关系?请直接写出结论;
(2)如图③,△ABC中,若AB=BC,那么(1)中的结论是否还成立?若成立,请给出证明:若不成立,请说明理由;
(3)如图④,△ABC中,若AB:BC=m:n,探索线段EM与EN的数量关系,并证明你的结论.

(年广西玉林、防城港12分)给定直线l:y=kx,抛物线C:y=ax2+bx+1.
(1)当b=1时,l与C相交于A,B两点,其中A为C的顶点,B与A关于原点对称,求a的值;
(2)若把直线l向上平移k2+1个单位长度得到直线r,则无论非零实数k取何值,直线r与抛物线C都只有一个交点.
①求此抛物线的解析式;
②若P是此抛物线上任一点,过P作PQ∥y轴且与直线y=2交于Q点,O为原点.求证:OP=PQ.