设数列{an}的首项a1∈(0,1),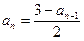 ,n=2,3,4,….(Ⅰ)求{an}的通项公式;(Ⅱ)设
,n=2,3,4,….(Ⅰ)求{an}的通项公式;(Ⅱ)设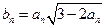 ,证明bn<bn+1,其中n为正整数.
,证明bn<bn+1,其中n为正整数.
△ABC的角A、B、C的对边分别为a、b、c,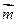 =(2b-c,a),
=(2b-c,a),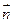 =(cosA,-cosC),且
=(cosA,-cosC),且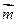 ⊥
⊥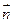 .(Ⅰ)求角A的大小;(Ⅱ)当y=2sin2B+sin(2B+
.(Ⅰ)求角A的大小;(Ⅱ)当y=2sin2B+sin(2B+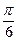 )取最大值时,求角
)取最大值时,求角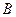 的大小.
的大小.
(Ⅰ)已知函数: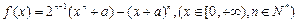 求函数
求函数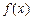 的最小值;
的最小值;
(Ⅱ)证明: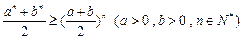 ;
;
(Ⅲ)定理:若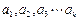 均为正数,则有
均为正数,则有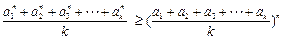 成立(其中
成立(其中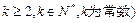 .请你构造一个函数
.请你构造一个函数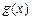 ,证明:
,证明:
当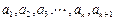 均为正数时,
均为正数时,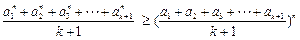 .
.
在东西方向直线延伸的湖岸上有一港口O,一艘机艇以40km/h的速度从O港出发,先沿东偏北的某个方向直线前进到达A处,然后改向正北方向航行,总共航行30分钟因机器出现故障而停在湖里的P处,由于营救人员不知该机艇的最初航向及何时改变的航向,故无法确定机艇停泊的准确位置,试划定一个最佳的弓形营救区域(用图形表示),并说明你的理由.
设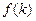 是满足不等式
是满足不等式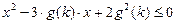 的自然数
的自然数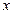 的个数,其中
的个数,其中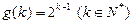 .
.
(Ⅰ)求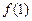 的值;
的值;
(Ⅱ) 求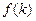 的解析式;
的解析式;
(Ⅲ)记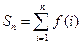 ,令
,令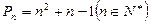 ,试比较
,试比较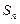 与
与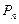 的大小.
的大小.