设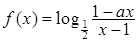 为奇函数,
为奇函数, 为常数。
为常数。
(I)求 的值;
的值;
(II)证明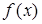 在区间
在区间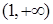 内单调递增;
内单调递增;
(III)若对于区间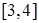 上的每一个
上的每一个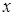 的值,不等式
的值,不等式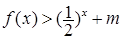 恒成立,求实数
恒成立,求实数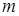 的取值范围。
的取值范围。
第30届夏季奥运会将于2012年7月27日在伦敦举行,当地某学校招募了8名男志愿者和12名女志愿者。将这20名志愿者的身高编成如下茎叶图(单位:cm):若身高在180cm以上(包括180cm)定义为“高个子”,身高在180cm以下(不包括180cm)定义为“非高个子”,且只有“女高个子”才能担任“礼仪小姐”。
(I)如果用分层抽样的方法从“高个子”和“非高个子”中抽取5人,再从这5人中选2人,那么至少有一人是“高个子”的概率是多少?
(Ⅱ)若从所有“高个子”中选3名志愿者,用X表示所选志愿者中能担任“礼仪小姐”的人数,试写出X的分布列,并求X的数学期望。
已知等差数列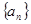 满足:
满足: .
.
(Ⅰ)求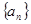 的通项公式;
的通项公式;
(Ⅱ)若 (
( ),求数列
),求数列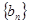 的前n项和
的前n项和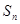 .
.
已知F1( 2,0),F2(2,0),点P满足|PF1|-|PF2|=2,记点P的轨迹为S,过点F2作直线
2,0),F2(2,0),点P满足|PF1|-|PF2|=2,记点P的轨迹为S,过点F2作直线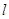 与轨迹S交于P、Q两点,过P、Q作直线x=的垂线PA、QB,垂足分别为A、B,记λ=|AP|·|BQ|.
与轨迹S交于P、Q两点,过P、Q作直线x=的垂线PA、QB,垂足分别为A、B,记λ=|AP|·|BQ|.
(1)求轨迹S的方程;
(2)设点M( 1,0),求证:当λ取最小值时,△PMQ的面积为9.
1,0),求证:当λ取最小值时,△PMQ的面积为9.
已知函数
(1)若x1=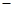 2和x2=4为函数f(x)的两个极值点,求函数
2和x2=4为函数f(x)的两个极值点,求函数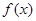 的表达式;
的表达式;
(2)若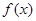 在区间[
在区间[ 1,3]上是单调递减函数,求
1,3]上是单调递减函数,求 的最小值.
的最小值.
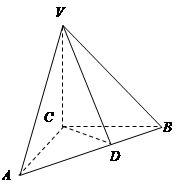
如图,在三棱锥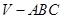 中,
中, 底面
底面 ,
, ,
,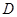 是
是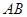 的中点,且
的中点,且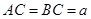 ,
,
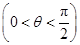 .
.
(1)求证:平面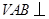 平面
平面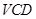 ;
;
(2)当角 变化时,求直线
变化时,求直线 与平面
与平面 所成的角的取值范围
所成的角的取值范围