奔跑的狗
苏步青是我国著名数学家、教育家，历任复旦大家教授、校长等职．1995年当选为中国科学院学部委员．苏步青的主要研究领域是微分几何学，他又是优秀的教学教育家，从事数学教学达60年，培养了大批数学人才．
一次在德国，苏步青与一位有名的数学家同乘电车时，这位数学家出了一道题目给苏教授解答．
这道题是：
甲乙两人同时从相距100千米的两地出发，相向而行，甲每小时走6千米，乙每小时走4千米，甲带了一只狗和他同时出发，狗以每小时10千米的速度向乙奔去，遇到乙即回头向甲奔去；遇到甲又回头向乙奔去，直到甲乙两人相遇时狗才停住．问这只狗共奔跑了多少千米路？
对这个问题，苏步青教授略加思索，就算出了正确的答案．请你也想一想，该怎么解答？
已知：如图，△ABC中，∠CAB＝90°，AC＝AB，点D、E是BC上的两点，且∠DAE＝45°，△ADC与△ADF关于直线AD对称．
（1）求证：△AEF≌△AEB；
（2）∠DFE＝ °．
操作题：
（1）已知：∠AOB，点M、N．
求作：①∠AOB的平分线OC；
②点P，在OC上，且PM=PN．（用尺规作图，保留作图痕迹，不写作法）
（2）如图，在3×3网格中，已知线段AB、CD，以格点为端点画一条线段，使它与AB、CD组成轴对称图形．（画出所有可能）
如图，点D在BC上，DE垂直平分AC，垂足为E，F是BA的中点．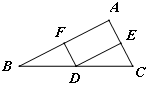
求证：DF是AB的垂直平分线．
结合数轴与绝对值的知识回答下列问题：
（1）数轴上表示4和1的两点之间的距离是 ；表示－3和2两点之间的距离是 ；一般地，数轴上表示数m和数n的两点之间的距离等于
．如果表示数a和－2的两点之间的距离是3，那么a＝ ；
（2）若数轴上表示数a的点位于－4与2之间，求
+
的值；
（3）当a取何值时，
+
+
的值最小，最小值是多少？请说明理由．
有一批水果，包装质量为每筐25千克，现抽取8筐样品进行检测，结果称重如下（单位：千克）：27，24，23，28，21，26，22，27，为了求得8筐样品的总质量，我们可以选取的一个恰当的基准数进行简化运算．
（1）你认为选取的一个恰当的基准数为 ；
（2）根据你选取的基准数，用正、负数填写上表；
| 原质量 |
27 |
24 |
23 |
28 |
21 |
26 |
22 |
27 |
| 与基准数的差距 |
（3）这8筐水果的总质量是多少？