已知动圆过定点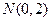
，且与定直线
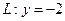相切.
（1）求动圆圆心的轨迹C的方程；
（2）若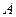
、
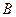是轨迹C上的两不同动点，且
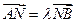. 分别以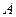、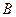为切点作轨迹C的切线，设其交点Q，证明
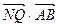为定值.
数列
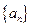中
，
，
（
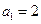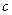是不为零的常数，
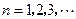），且
成等比数列．
（1）求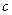的值；
（2）求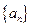的通项公式；
（3）求数列
的前
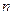项之和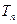
已知：函数
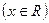
⑴
求
的最小正周期；
⑵求的单递增区间；
⑶求图象的对称轴、对称中心。
如图，在四棱锥P—ABCD中，底面ABCD为矩形，侧棱PA⊥底面ABCD，AB=
，BC=
1，PA=2，E为PD的中点.
（1）求直线AC与PB所
成角的余弦值；
（2）在侧面PAB内找一点N，使NE⊥面PAC，并求出N点
到AB和AP的距离.
已知向量
，若正数k和t使得向量
垂直，求k的最小值.
是函数
图象的一条对称轴．
的值；
在
上的图象简图（不要求书写作图过程）． 