(本小题10分)如图，已知平行四边形ABCD和矩形ACEF所在的平面互相垂直，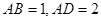
，
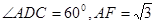
（1）求证：AC⊥BF；
（2）求点A到平面FBD的距离.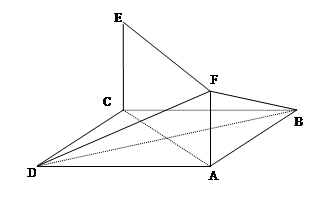 
已知函数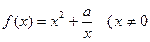
，常数
．
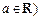（1）当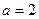
时，解不等式
；
（2）讨论函数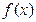
的奇偶性，并说明理由．
（3）（理做文不做）若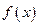
在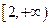
是增函数，求实数
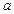的范围
已知函数f(x)=ax3+x2-x (a∈R且a≠0)
（1）若函数f(x)在（2，+∞）上存在单调递增区间，求a的取值范围.
（2）证明：当a>0时，函数在f(x)在区间（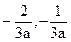
）上不存在零点
设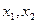
是函数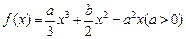
的两个极值点，且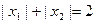
（Ⅰ）求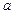
的取值范围；
（Ⅱ）求证：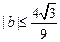
.
已知函数f(x)=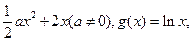
(1)若h(x)=f(x)-g(x)存在单调增区间，求a的取值范围；
(2)是否存在实数a>0，使得方程
在区间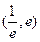
内有且只有两个不相等的实数根？若存在，求出a的取值范围？若不存在，请说明理由。
已知函数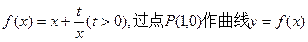
的两条切线PM、PN，切点分别为M、N.
（I）当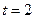
时，求函数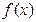
的单调递增区间；
（II）设|MN|=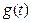
，试求函数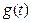的表达式；
（III）在（II）的条件下，若对任意的正整数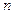
，在区间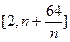
内，总存在m＋1个数
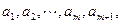使得不等式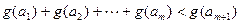
成立，求m的最大值.