某礼堂共有25排座位,第一排有20个座位,后面每一排都比前一排多1个座位,写出每排的座位数m与这排的排数n的函数关系式并写出自变量n的取值范围.
上题中,在其他条件不变的情况下,请探究下列问题:
①当后面每一排都比前一排多2个座位时,则每排的座位数m与这排的排数n的函数关系式是______________(1≤n≤25,且n是正整数)
②当后面每一排都比前一排多3个座位、4个座位时,则每排的座位数m与这排的排数n的函数关系式分别是___________,___________(1≤n≤25,且n是正整数)
③某礼堂共有P排座位,第一排有a个座位,后面每一排都比前一排多b个座位,试写出每排的座位数m与这排的排数n的函数关系式,并写出自变量n的取值范围.
某百货大楼服装柜在销售中发现:“宝乐”牌童装平 均每天可售出20件,每件盈利40元。为了迎接“十·一”国庆节,商场决定采取适当的降价措施,扩大销售量,增加盈利,尽快减少库存。经市场调查发现:如果每件童装降价4元,那么平均每天就可多售出8件。要想平均每天在销售这种童装上盈利1200元,那么每件童装应降价多少?
均每天可售出20件,每件盈利40元。为了迎接“十·一”国庆节,商场决定采取适当的降价措施,扩大销售量,增加盈利,尽快减少库存。经市场调查发现:如果每件童装降价4元,那么平均每天就可多售出8件。要想平均每天在销售这种童装上盈利1200元,那么每件童装应降价多少?
已知关于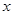 的方程
的方程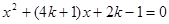 。
。(1)求证此方程一定有两个不
 相等的实数根。
相等的实数根。(2)设
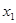 、
、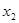 是方程的两个实数根,且(
是方程的两个实数根,且(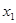 -2)(
-2)(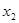 -2)=2
-2)=2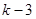 ,求
,求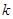 的值。
的值。
如图所示,在一 块长为32米,宽为15米的矩形草地上,在中间要设计一横二竖的等宽的、供居
块长为32米,宽为15米的矩形草地上,在中间要设计一横二竖的等宽的、供居 民散步的小路,要使小路的面积是总面积的八分之一,请问小路的宽应是多少米?
民散步的小路,要使小路的面积是总面积的八分之一,请问小路的宽应是多少米?
如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,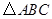 的顶点均在格点上,点
的顶点均在格点上,点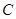 的坐标为
的坐标为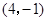 .
.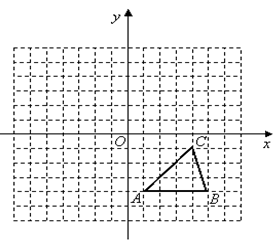
①把
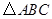 向上平移5个单位后得到对应的
向上平移5个单位后得到对应的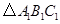 ,画出
,画出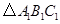 ,并写出
,并写出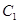 的坐标;
的坐标;②以原点
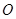 为对称中心,再画出与
为对称中心,再画出与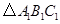 关于原点
关于原点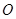 对称的
对称的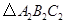 ,并写出点
,并写出点 的坐标.
的坐标.
已知a、b、c满足
求:(1)a、b、c的值;
(2)试问以a、b、c为 边能否构成三角形?若能构成三角形,求出三角形的周长;
边能否构成三角形?若能构成三角形,求出三角形的周长;
若不能构成三角形,请说明理由.