选修4-4:坐标系与参数方程
在平面直角坐标系xOy中,直线l的参数方程为 (t为参数),直线l与曲线
(t为参数),直线l与曲线 交于A,B两点.
交于A,B两点.
(1)求 的长;
的长;
(2)在以O为极点,x轴的正半轴为极轴建立极坐标系,设点P的极坐标为 ,求点P到线段AB中点M的距离.
,求点P到线段AB中点M的距离.
选修4-1:几何证明选讲
如图,正方形ABCD边长为2,以D为圆心,DA为半径的圆弧与以BC为直径的半圆O交于点F,连接CF并延长交AB于点E.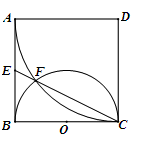
(1)求证:AE=EB;
(2)求 的值.
的值.
已知函数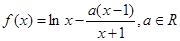 .
.
(1)若x=2是函数f(x)的极值点,求曲线y=f(x)在点(1,f(1))处的切线方程;
(2)若函数f(x)在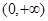 上为单调增函数,求a的取值范围;
上为单调增函数,求a的取值范围;
(3)设m,n为正实数,且m>n,求证: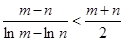 .
.
已知A、B分别是椭圆 的左右顶点,右焦点与抛物线
的左右顶点,右焦点与抛物线 的焦点F重合.
的焦点F重合.
(1)求椭圆C的方程;
(2)已知点P是椭圆C上异于A、B的动点,直线l过点A且垂直于x轴,若过F作直线FQ垂直于AP,并交直线l于点Q,证明:Q、P、B三点共线.
如图所示,AD⊥平面ABC,CE⊥平面ABC,AC=AD=AB=1, ,凸多面体ABCED的体积为
,凸多面体ABCED的体积为 ,F为BC的中点.
,F为BC的中点.
(1)求证:AF∥平面BDE;
(2)求证:平面BDE⊥平面BCE.