已知,如图,∠1=∠2,且∠1=∠3,阅读并补充下列推理过程,在括号中填写理由: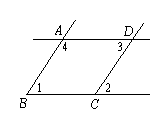
解:∵∠1=∠2( )
∴ ∥ ( )
又∵∠1=∠3(已知)
∴∠2=∠3
∴ ∥ ( )
∴∠1+∠4=180° ( )
某校团委计划在“七·一”前夕举行“唱响红歌”班级歌咏比赛,要确定一首喜欢人数最多的歌曲为每班必唱歌曲.为此提供代号为A、B、C、D四首备选曲目让学生选择,经过抽样调查,并将采集的数据绘制如下两幅不完整的统计图.请根据图①,图②所提供的信息,解答下列问题:
(1)本次抽样调查的学生有_________名,其中选择曲目代号为A的学生占抽样总数的百分比是________%.
(2)请将图②补充完整;
(3)扇形图中选择曲目代号为B的学生所在的扇形的圆心角的度数是 .
(4)若该校共有1200名学生,根据抽样调查的结果估计全校共有多少名学生选择此必唱歌曲?(要有解答过程)
已知如图(1),⊙O的直径AB=12cm,AM和BN是它的两条切线,DE切⊙O于E,交AM于D,交BN于C.

(1)设AD=m,BC=n,若m、n是方程 的两个根,求m、n.
的两个根,求m、n.
(2) 如图(2),连接OD、BE,求证:OD∥BE.
如图,AB是⊙O的直径,AC是弦,CD是⊙O的切线,C为切点,AD⊥CD于点D.
求证:(1)∠AOC=2∠ACD;(2)AC2=AB·AD.
如图,ABCD是⊙O的内接四边形,DP∥AC,交BA的延长线于P,求证:AD·DC=PA·BC.
阅读下列材料,然后解答问题.
经过正四边形(即正方形)各顶点的圆叫做这个正四边形的外接圆,圆心是正四边形的对称中心,这个正四边形叫做这个圆的内接正四边形.
如图,正方形ABCD内接于⊙O,⊙O的面积为S1,正方形ABCD的面积为S2.以圆心O为顶点作∠MON,使∠MON=90°.将∠MON绕点O旋转,OM、ON分别与⊙O交于点E、F,分别与正方形ABCD的边交于点G、H.设由OE、OF、 及正方形ABCD的边围成的图形(阴影部分)的面积为S.
及正方形ABCD的边围成的图形(阴影部分)的面积为S.
(1)当OM经过点A时(如图①),则S、S1、S2之间的关系为: (用含S1、S2的代数式表示);
(2)当OM⊥AB于G时(如图②),则(1)中的结论仍然成立吗?请说明理由;
(3)当 旋转到任意位置时(如图③),则(1)中的结论仍然成立吗?请说明理由;
旋转到任意位置时(如图③),则(1)中的结论仍然成立吗?请说明理由;