计算: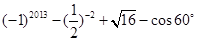 .
.
如图 ,在平面直角坐标系中,等腰直角
,在平面直角坐标系中,等腰直角 的斜边
的斜边 在
在 轴上,顶点
轴上,顶点 的坐标为
的坐标为 ,
, 为斜边上的高.抛物线
为斜边上的高.抛物线 与直线
与直线 交于点
交于点 ,点
,点 的横坐标为
的横坐标为 .点
.点 在
在 轴的正半轴上,过点
轴的正半轴上,过点 作
作 轴.交射线
轴.交射线 于点
于点 .设点
.设点 的横坐标为
的横坐标为 ,以
,以 为顶点的四边形的面积为
为顶点的四边形的面积为 .
.
(1)求 所在直线的解析式;
所在直线的解析式;
(2)求 的值;
的值;
(3)当 时,求
时,求 与
与 的函数关系式;
的函数关系式;
(4)如图 ,设直线
,设直线 交射线
交射线 于点
于点 ,交抛物线于点
,交抛物线于点 .以
.以 为一边,在
为一边,在 的右侧作矩形
的右侧作矩形 ,其中
,其中 .直接写出矩形
.直接写出矩形 与
与 重叠部分为轴对称图形时
重叠部分为轴对称图形时 的取值范围.
的取值范围.
某商店经营儿童益智玩具,已知成批购进时的单价是20元.调查发现:销售单价是30元时,月销售量是230件,而销售单价每上涨1元,月销售量就减少10件,但每件玩具售价不能高于40元. 设每件玩具的销售单价上涨了x元时(x为正整数),月销售利润为y元.
(1)求y与x的函数关系式并直接写出自变量x的取值范围;
(2)每件玩具的售价定为多少元时,月销售利润恰为2520元?
(3)每件玩具的售价定为多少元时可使月销售利润最大?最大的月利润是多少?
如图,△ABC内接于⊙O,直径BD交AC于E,过O作FG⊥AB,交AC于F,交AB于H,交⊙O于G.
(1)求证:OF•DE=2OE•OH;
(2)若⊙O的半径为12,且OE:OF:OD=2:3:6,求阴影部分的面积.(结果保留根号)
如图, 为正方形
为正方形 边
边 上任一点,
上任一点, 于点
于点 ,在
,在 的延长线上取点
的延长线上取点 ,使
,使 ,连接
,连接 ,
, .
.
(1)求证: ;
;
(2) 的平分线交
的平分线交 于
于 点,连接
点,连接 ,求证:
,求证: ;
;