在▱ABCD中,设边AB、BC、CD的中点分别为E、F、G,设DF与AG、EG的交点分别为H、K,设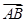 =a,
=a,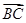 =b,试用a、b表示
=b,试用a、b表示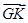 、
、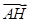 .
.
已知函数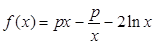 .
.
(1)若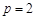 ,求曲线
,求曲线 在点
在点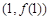 处的切线方程;
处的切线方程;
(2)若函数 在其定义域内为增函数,求正实数
在其定义域内为增函数,求正实数 的取值范围;
的取值范围;
(3)设函数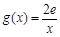 ,若在
,若在 上至少存在一点
上至少存在一点 ,使得
,使得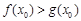 成立,求实数
成立,求实数 的取值范围.
的取值范围.
已知椭圆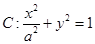 经过点
经过点 .
.
(1)求椭圆 的方程及其离心率;
的方程及其离心率;
(2)过椭圆右焦点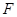 的直线(不经过点
的直线(不经过点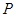 )与椭圆交于
)与椭圆交于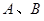 两点,当
两点,当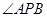 的平分线为
的平分线为 时,求直线
时,求直线 的斜率
的斜率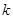 .
.
一个袋中装有8个大小质地相同的球,其中4个红球、4个白球,现从中任意取出四个球,设X为取得红球的个数.
(1)求X的分布列;
(2)若摸出4个都是红球记5分,摸出3个红球记4分,否则记2分.求得分的期望.
如图,在四棱锥 中,底面
中,底面 是正方形,侧棱
是正方形,侧棱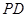 ⊥底面
⊥底面 ,
, ,
, 是
是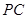 的中点,作
的中点,作 交
交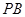 于点
于点 .
.
(1)求证:
 平面
平面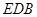 ;
;
(2)求二面角 的正弦值.
的正弦值. 
已知数列 的前
的前 项和为
项和为 ,且
,且 .
.
(1)求数列 的通项公式;
的通项公式;
(2)设 ,求数列
,求数列 的前
的前 项和
项和 .
.