在△OAB中,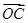 =
=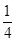
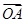 ,
,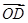 =
=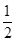
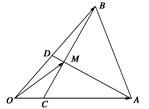
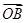 ,AD与BC交于点M,设
,AD与BC交于点M,设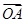 =a,
=a,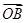 =b,以a、b为基底表示
=b,以a、b为基底表示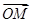 .
.
(本小题满分14分)设平面向量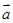 =
= ,
,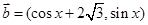 ,
,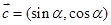 ,
,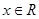 .
.
(1)若 ,求
,求 的值;
的值;
(2)若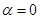 ,求函数
,求函数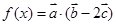 的最大值,并求出相应的
的最大值,并求出相应的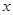 值.
值.
选修4-5:不等式选讲
设函数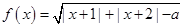 .
.
(Ⅰ)当a=5时,求函数f(x)的定义域;
(Ⅱ)若函数f(x)的定义域为R,试求a的取值范围.
选修4-4:坐标系与参数方程
已知曲线C的极坐标方程为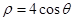 ,以极点为原点,极轴为
,以极点为原点,极轴为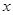 轴的正半轴建立平面直角
轴的正半轴建立平面直角
坐标系,设直线l的参数方程为 (t为参数).
(t为参数).
(Ⅰ)求曲线C的直角坐标方程与直线l的普通方程;
(Ⅱ)设曲线C与直线l相交于P,Q两点,以PQ为一条边作曲线C的内接矩形,求该矩形的面积.
已知函数 .
.
(Ⅰ)当a=1时,求曲线y=f(x0在x=1处的切线方程;
(Ⅱ)求函数f(x)在区间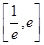 上的最小值;
上的最小值;
(Ⅲ)若关于 的方程
的方程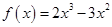 在区间
在区间 内有两个不相等的实数根,求实数a的取值范围.
内有两个不相等的实数根,求实数a的取值范围.
已知椭圆 (a>b>0)的两个焦点分别为
(a>b>0)的两个焦点分别为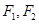 ,离心率为
,离心率为 ,过
,过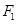 的直线l与椭圆C交于M,N两点,且
的直线l与椭圆C交于M,N两点,且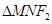 的周长为8.
的周长为8.
(Ⅰ)求椭圆C的方程;
(Ⅱ)过原点O的两条互相垂直的射线与椭圆C分别交于A,B两点,证明:点O到直线AB的距离为定值,并求出这个定值.