（本小题满分14分）设平面向量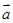
＝
，
，
，
．
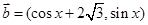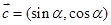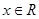（1）若
，求
的值；
（2）若
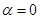，求函数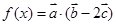
的最大值，并求出相应的
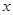值．
(13分)已知向量
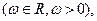设函数
若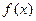
的最小正周期为
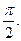(1)求
的值；(2)求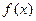的单调区间.
已知二次函数
。
（1）若任意x1，x2∈R，且
，都有
，求证：关于x的方程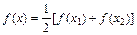
有两个不相等的实数根且必有一个根属于（
）；
（2）若关于x的方程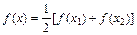在（）的根为m，且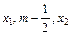
成等差数列，设函数f (x)的图象的对称轴方程为
，求证：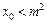
。
已知函数f(x)=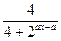
在[0，1]上的最小值为
，
（1）求f(x)的解析式；（2）证明：f(1)+f(2)+…+f(n)＞n-+
(n∈N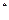
)
F1、F2为双曲线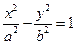
的左右焦点，O为坐标原点，P在双曲线的左支上，点M在右准线上，且满足：
，
（λ＞0）
（1）求此双曲线的离心率；
（2）若过点N（
，
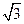）的双曲线C的虚轴端点分别为B1、B2（B1在y轴正半轴上），点A、B在双曲线上，且
，
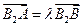，求双曲线C和直线AB的方程。
已知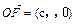
（c>0），
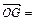（n, n）（n∈R）, 
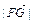的最小值为1，若动点P同时满足下列三个条件：①
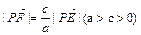，②
（其中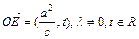
）；③动点P的轨迹C经过点B（0,－1）。
（1）求c值；（2）求曲线C的方程；（3）方向向量为
的直线l与曲线C交于不同两点M、N，若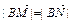
，求k的取值范围。