已知椭圆 (a>b>0)的两个焦点分别为
(a>b>0)的两个焦点分别为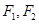 ,离心率为
,离心率为 ,过
,过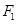 的直线l与椭圆C交于M,N两点,且
的直线l与椭圆C交于M,N两点,且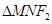 的周长为8.
的周长为8.
(Ⅰ)求椭圆C的方程;
(Ⅱ)过原点O的两条互相垂直的射线与椭圆C分别交于A,B两点,证明:点O到直线AB的距离为定值,并求出这个定值.
设集合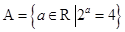 ,
,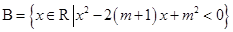 .
.
(1)若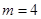 ,求
,求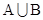 ;
;
(2)若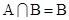 ,求实数
,求实数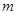 的取值范围.
的取值范围.
设函数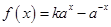 (
(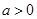 且
且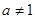 )是奇函数.
)是奇函数.
(1)求常数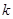 的值;
的值;
(2)若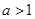 ,试判断函数
,试判断函数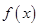 的单调性,并加以证明;
的单调性,并加以证明;
(3)若 ,且函数
,且函数 在区间
在区间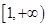 上的最小值为
上的最小值为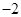 ,求实数
,求实数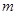 的值.
的值.
已知函数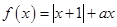 (
(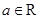 ).
).
(1)当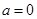 ,
, 时,分别画出函数
时,分别画出函数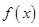 的图象;
的图象;
(2)若函数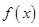 是
是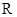 上的单调函数,求实数
上的单调函数,求实数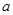 的取值范围.
的取值范围.
两个重要城市之间人员交流频繁,为了缓解交通压力,特修一条专用铁路,用一列火车作为交通车.已知该火车每日往返的次数 是车头每次拖挂车厢节数
是车头每次拖挂车厢节数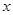 的一次函数.若车头拖挂
的一次函数.若车头拖挂 节车厢,则每日能往返
节车厢,则每日能往返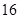 次;若车头每次拖挂
次;若车头每次拖挂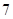 节车厢,则每日能往返
节车厢,则每日能往返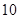 次.
次.
(1)求此一次函数;
(2)求这列火车每天运营的车厢总节数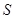 关于
关于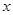 的函数;
的函数;
(3)若每节车厢能载旅客 人,求每次车头拖挂多少节车厢可使每天运送的旅客人数最多,并求出每天最多运送旅客人数.
人,求每次车头拖挂多少节车厢可使每天运送的旅客人数最多,并求出每天最多运送旅客人数.
对于函数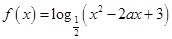 ,解答下述问题:
,解答下述问题:
(1)若函数的定义域为 ,求实数
,求实数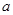 的取值范围;
的取值范围;
(2)若函数的值域为 ,求实数
,求实数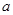 的值.
的值.