已知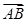 =(6,1),
=(6,1),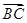 =(x,y),
=(x,y),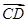 =(-2,-3),若
=(-2,-3),若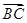 ∥
∥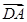 ,
,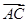 ⊥
⊥ .
.
(1)求x、y的值;
(2)求四边形ABCD的面积.
已知 =1,
=1, =2,
=2, 与
与 的夹角为60°。
的夹角为60°。
(1)求: ,(
,(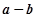 )·(
)·( );(2)求:
);(2)求: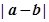 。
。
已知方程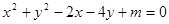 ,
,
(1)若此方程表示圆,求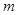 的取值范围;
的取值范围;
(2)若(1)中的圆与直线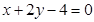 相交于
相交于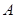 、
、 两点,且
两点,且 (
(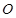 为坐标原点),求
为坐标原点),求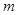 的值;
的值;
(3)在(2)的条件下,求以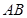 为直径的圆的方程。
为直径的圆的方程。
已知圆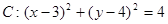 和直线
和直线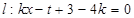 ,
,
(1)求证:不论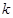 取什么值,直线和圆总相交;
取什么值,直线和圆总相交;
(2)求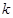 取何值时,直线被圆截得的弦最短,并求出最短弦的长;
取何值时,直线被圆截得的弦最短,并求出最短弦的长;
如图,在四棱锥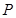 -
- 中,底面
中,底面 是边长为
是边长为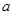 的正方形,
的正方形,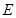 、
、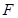 分别为
分别为 、
、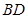 的中点,侧面
的中点,侧面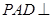 底面
底面 ,且
,且 。
。
(Ⅰ)求证: 平面
平面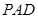 ;
;
(Ⅱ)求证:平面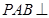 平面
平面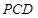 ;
;
(Ⅲ)求三棱锥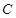 -
-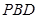 的体积。
的体积。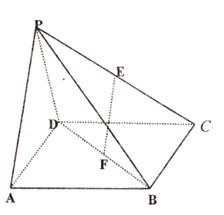
已知点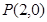 ,及⊙
,及⊙ :
: 。
。
(Ⅰ)当直线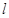 过点
过点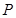 且与圆心
且与圆心 的距离为1时,求直线
的距离为1时,求直线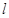 的方程;
的方程;
(Ⅱ)设过点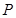 的直线与⊙
的直线与⊙ 交于
交于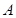 、
、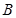 两点,当
两点,当 ,求以线段
,求以线段 为直径的圆的方程。
为直径的圆的方程。