设 ,其中
,其中 ,
,
如果 ,求实数
,求实数 的取值范围
的取值范围
已知函数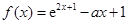 ,
,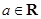 .
.
(Ⅰ)若曲线 在点
在点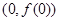 处的切线与直线
处的切线与直线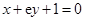 垂直,求
垂直,求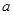 的值;
的值;
(Ⅱ)求函数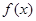 的单调区间;
的单调区间;
(Ⅲ)设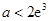 ,当
,当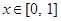 时,都有
时,都有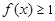 成立,求实数
成立,求实数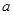 的取值范围.
的取值范围.
如图,在四棱锥 中,底面
中,底面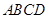 是正方形,侧面
是正方形,侧面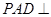 底面
底面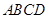 ,
,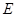 ,
, 分别为
分别为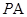 ,
,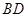 中点,
中点,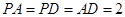 .
.
(Ⅰ)求证: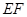 ∥平面
∥平面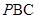 ;
;
(Ⅱ)求二面角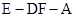 的余弦值;
的余弦值;
(Ⅲ)在棱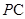 上是否存在一点
上是否存在一点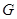 ,使
,使 平面
平面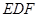 ?若存在,指出点
?若存在,指出点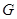 的位置;若不存在,说明理由.
的位置;若不存在,说明理由.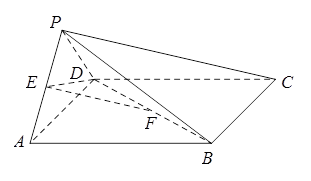
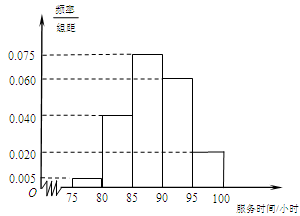
某市规定,高中学生三年在校期间参加不少于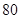 小时的社区服务才合格.教育部门在全市随机抽取200位学生参加社区服务的数据,按时间段
小时的社区服务才合格.教育部门在全市随机抽取200位学生参加社区服务的数据,按时间段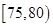 ,
,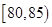 ,
,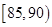 ,
,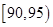 ,
,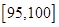 (单位:小时)进行统计,其频率分布直方图如图所示.
(单位:小时)进行统计,其频率分布直方图如图所示.
(Ⅰ)求抽取的200位学生中,参加社区服务时间不少于90小时的学生人数,并估计
从全市高中学生中任意选取一人,其参加社区服务时间不少于90小时的概率;
(Ⅱ)从全市高中学生(人数很多)中任意选取3位学生,记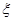 为3位学生中参加社区服务时间不少于90小时的人数.试求随机变量
为3位学生中参加社区服务时间不少于90小时的人数.试求随机变量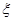 的分布列和数学期望
的分布列和数学期望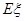 .
.
在△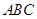 中,角
中,角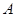 ,
,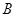 ,
,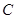 的对边分别是
的对边分别是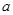 ,
,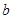 ,
,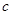 ,且
,且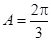 ,
, ,△
,△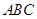 的面积为
的面积为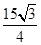 .
.
(Ⅰ)求边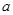 的长;
的长;
(Ⅱ)求 的值.
的值.
已知函数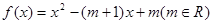 .
.
(1)对任意实数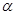 ,恒有
,恒有 ,证明
,证明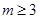 ;
;
(2)若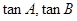 是方程
是方程 的两个实根,
的两个实根, 是锐角三角形的两个内角,求证:
是锐角三角形的两个内角,求证: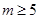 。
。