某校从参加高一年级期末考试的学生中抽出40名学生，将其成绩（均为整数）分成六段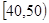
，
…
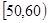后画出如下部分频率分布直方图，观察图形的信息，回答下列问题：
（1）求第四小组的频率，并补全频率分布直方图；
（2）估计这次考试的及格率（60分及以上为及格）和平均分；
（3）从成绩是40～50分及90～100分的学生中选两人，记他们的成绩为x，y，求满足“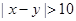
”的概率.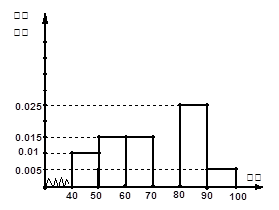
（本小题满分14分）
已知曲线
在点
处的切线斜率为
（1）求
的极值；
（2）设
在（-∞，1）上是增函数，求实数
的取值范围；
（3）若数列
满足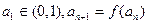
，求证：对一切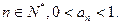
（本小题满分12分）
在平面直角坐标系
中有两定点
，
，若动点M满足
，设动点M的轨迹为C。
（1）求曲线C的方程；
（2）设直线
交曲线C于A、B两点，交直线
于点D，若
，证明：D为AB的中点。
（本小题满分12分）
已知四棱锥P—ABCD中，
平面ABCD，底面ABCD为菱形，
，AB=PA=2，E、F分别为BC、PD的中点。
（1）求证：PB//平面AFC；
（2）求平面PAE与平面PCD所成锐二面角的余弦值。
（本小题满分12分）
已知等差数列
是递增数列，且满足
（1）求数列的通项公式；
（2）令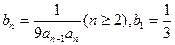
，求数列
的前
项和
（本小题满分12分）
已知集合
（1）若
；
（2）若
的充分条件，求实数
的取值范围。