(本小题满分12分)
在直角坐标系中,已知 ,
, ,
, 为坐标原点,
为坐标原点,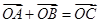 ,
,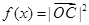 .
.
(Ⅰ)求 的对称中心的坐标及其在区间
的对称中心的坐标及其在区间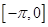 上的单调递减区间;
上的单调递减区间;
(Ⅱ)若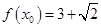 ,
,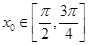 ,求
,求 的值。
的值。
设A={1,2,3,4},B={1,2},试求集合C,使C真包含于A且B包含于C
确定整数x,y,使{2x,x+y}={7,4}
已知数列 中,
中, ,
, ,对任意
,对任意 有
有 成立.
成立.
(I)若 是等比数列,求
是等比数列,求 的值;
的值;
(II)求数列 的通项公式;
的通项公式;
(III)证明: 对任意
对任意 成立.
成立.
在平面直角坐标系 中,设二次函数
中,设二次函数 的图象与两坐标轴有三个不同的交点. 经过这三个交点的圆记为
的图象与两坐标轴有三个不同的交点. 经过这三个交点的圆记为 .
.
(I)求实数 的取值范围;
的取值范围;
(II)求圆 的一般方程;
的一般方程;
(III)圆 是否经过某个定点(其坐标与
是否经过某个定点(其坐标与 无关)?若存在,请求出点点的坐标;若不存在,请说明理由.
无关)?若存在,请求出点点的坐标;若不存在,请说明理由.
如图所示,港口 北偏东
北偏东 方向的点
方向的点 处有一观测站,港口正东方向的
处有一观测站,港口正东方向的 处有一轮船,测得
处有一轮船,测得 为
为 海里. 该轮船从
海里. 该轮船从 处沿正西方向航行
处沿正西方向航行 海里后到达
海里后到达 处,测得
处,测得 为
为 海里. 问此时轮船离港口
海里. 问此时轮船离港口 还有多少海里?
还有多少海里?