（本小题满分14分）某种商品的成本为5元/ 件，开始按8元/件销售，销售量为50件，为了获得最大利润，商家先后采取了提价与降价两种措施进行试销。经试销发现：销售价每上涨1元每天销售量就减少10件；而降价后，日销售量Q（件）与实际销售价x（元）满足关系：
|
[
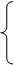
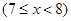[已知直线l与两坐标轴围成的三角形的面积为3，分别求满足下列条件的直线l的方程：
（1）过定点A（﹣3，4）；
（2）斜率为
．
在△ABC中，已知点A（5，﹣2）、B（7，3），且边AC的中点M在y轴上，边BC的中点N在x轴上．
（1）求点C的坐标；
（2）求直线MN的方程．
（1）求经过点A（﹣5，2）且在x轴上的截距等于在y轴上的截距的2倍的直线方程．
（2）过点A（8，6）引三条直线l1，l2，l3，它们的倾斜角之比为1：2：4，若直线l2的方程是y=
x，求直线l1，l3的方程．
△ABC的三个顶点为A（﹣3，0），B（2，1），C（﹣2，3），求：
（1）BC所在直线的方程；
（2）BC边上中线AD所在直线的方程；
（3）BC边上的垂直平分线DE的方程．
如图，圆周上点A依逆时针方向做匀速圆周运动．已知A点1分钟转过θ（0＜θ＜π）角，2分钟到达第三象限，14分钟后回到原来的位置，求θ．