求与直线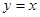 相切
相切 圆心在直线
圆心在直线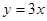 上且被
上且被 轴截得的弦长为
轴截得的弦长为 的圆的方程
的圆的方程
(本小题满分12分)某高中数学竞赛培训在某学段共开设有初等代数、平面几何、初等数论和微积分初步共四门课程,要求初等数论、平面几何都要合格,且初等代数和微积分初步至少有一门合格,则能取得参加数学竞赛复赛的资格.现有甲、乙、丙三位同学报名参加数学竞赛培训,每一位同学对这四门课程考试是否合格相互独立,其合格的概率均相同(见下表),且每一门课程是否合格相互独立.
(Ⅰ)求甲同学取得参加数学竞赛复赛的资格的概率;
(Ⅱ)记 表示三位同学中取得参加数学竞赛复赛的资格的人数,求
表示三位同学中取得参加数学竞赛复赛的资格的人数,求 的分布列及期望
的分布列及期望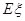 .
.
已知函数 ,
, .
.
(1)已知 在
在 上是单调函数,求
上是单调函数,求 的取值范围;
的取值范围;
(2)已知 满足
满足 ,且
,且 ,试比较
,试比较 与
与 的大小;
的大小;
(3)已知 ,是否存在正数
,是否存在正数 ,使得关于
,使得关于 的方程
的方程 在
在 上有两个不相等的实数根?如果存在,求
上有两个不相等的实数根?如果存在,求 满足的条件;如果不存在,说明理由.
满足的条件;如果不存在,说明理由.
已知椭圆C: 的离心率为
的离心率为 ,
, 是椭圆的两个焦点,
是椭圆的两个焦点, 是椭圆上任意一点,且
是椭圆上任意一点,且 的周长是
的周长是 .
.
(1)求椭圆C的方程;
(2)设圆T: ,过椭圆的上顶点作圆T的两条切线交椭圆于E、F两点,当圆心在
,过椭圆的上顶点作圆T的两条切线交椭圆于E、F两点,当圆心在 轴上移动且
轴上移动且 时,求
时,求 的斜率的取值范围.
的斜率的取值范围.
某公司从大学招收毕业生,经过综合测试,录用了14名男生和6名女生,这20名毕业生的测试成绩如茎叶图所示(单位:分).公司规定:成绩在180分以上者到甲部门工作,180分以下者到乙部门工作,另外只有成绩高于180分的男生才能担任助理工作.
(1)如果用分层抽样的方法从甲部门人选和乙部门人选中选取8人,再从这8人中选3人,那么至少有一人是甲部门人选的概率是多少?
(2)若从所有甲部门人选中随机选3人,用X表示所选人员中能担任助理工作的人数,写出X的分布列,并求出X的数学期望.
如图,在四棱锥 中,
中, 底面
底面 ,底面
,底面 是梯形,其中
是梯形,其中 ,
, ,
, 与
与 交于点
交于点 ,
, 是
是 边上的点,且
边上的点,且 ,已知
,已知 ,
, ,
, .
.
(1)求平面 与平面
与平面 所成锐二面角的正切;
所成锐二面角的正切;
(2)已知 是
是 上一点,且
上一点,且 平面
平面 ,求
,求 的值.
的值.