如图,甲船以每小时 海里的速度向正北方航行,乙船按固定方向匀速直线航行,当甲船位于
海里的速度向正北方航行,乙船按固定方向匀速直线航行,当甲船位于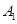 处时,乙船位于甲船的北偏西
处时,乙船位于甲船的北偏西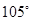 方向的
方向的 处,此时两船相距
处,此时两船相距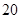 海里,当甲船航行
海里,当甲船航行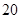 分钟到达
分钟到达 处时,乙船航行到甲船的北偏西
处时,乙船航行到甲船的北偏西 方向的
方向的 处,此时两船相距
处,此时两船相距 海里,问乙船每小时航行多少海里?(结论保留根号形式)
海里,问乙船每小时航行多少海里?(结论保留根号形式)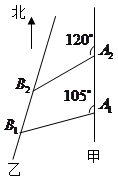
(本小题满分10分)选修4—4:坐标系与参数方程
已知倾斜角为 的直线
的直线 经过点P(1,1).
经过点P(1,1).
(Ⅰ)写出直线 的参数方程;
的参数方程;
(Ⅱ)设直线 与直线
与直线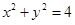 相交于
相交于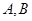 两点,求
两点,求 的值.
的值.
(本小题满分10分)选修4—1:几何证明选讲
如图,已知△ABC的两条角平分线AD和CE相交于H,B,E,H,D四点共圆,F在AC上,且∠DEC=∠FEC.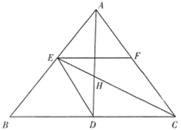
(Ⅰ)求∠B的度数;
(Ⅱ)证明:AE=4F.
(本小题满分12分)设函数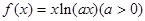
(Ⅰ)设 ,讨论函数F(x)的单调性;
,讨论函数F(x)的单调性;
(Ⅱ)过两点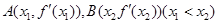 的直线的斜率为
的直线的斜率为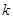 ,求证:
,求证: .
.
(本小题满分12分)已知椭圆 ,左焦点到直线x一y一2=0的距离为
,左焦点到直线x一y一2=0的距离为 ,左焦点到左顶点的距离为
,左焦点到左顶点的距离为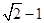 .
.
(Ⅰ)求椭圆的方程;
(Ⅱ)直线l过点M(2,0)交椭圆于A,B两点,是否存在点N(t,0),使得 ,若存在,求出t的取值范围;若不存在,说明理由.
,若存在,求出t的取值范围;若不存在,说明理由.
(本小题满分12分)如图,四棱锥S一ABCD中,已知AD∥BC,∠ASC=60°,∠BAD=135°,AD=DC= ,SA=SC=SD=2.
,SA=SC=SD=2.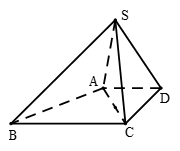
(Ⅰ)求证:AC⊥SD;
(Ⅱ)求二面角A - SB -C的余弦值.