某普通高中共有教师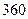 人,分为三个批次参加研修培训,在三个批次中男、女教师人数如下表所示:
人,分为三个批次参加研修培训,在三个批次中男、女教师人数如下表所示:
| |
第一批次 |
第二批次 |
第三批次 |
| 女教师 |
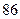 |
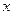 |
 |
| 男教师 |
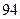 |
 |
 |
已知在全体教师中随机抽取1名,抽到第二、三批次中女教师的概率分别是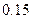 、
、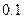 .
.
(1)求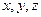 的值;
的值;
(2)为了调查研修效果,现从三个批次中按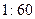 的比例抽取教师进行问卷调查,三个批次被选取的人数分别是多少?
的比例抽取教师进行问卷调查,三个批次被选取的人数分别是多少?
(3)若从(2)中选取的教师中随机选出两名教师进行访谈,求参加访谈的两名教师“分别来自两个批次”的概率.
已知数列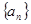 具有性质:①
具有性质:① 为正数;②对于任意的正整数
为正数;②对于任意的正整数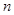 ,当
,当 为偶数时,
为偶数时, ;当
;当 为奇数时,
为奇数时,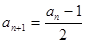
(1)若 ,求数列
,求数列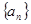 的通项公式;
的通项公式;
(2)若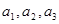 成等差数列,求
成等差数列,求 的值;
的值;
(3)设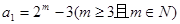 ,数列
,数列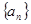 的前
的前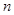 项和为
项和为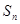 ,求证:
,求证:
已知函数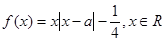 .
.
(1)当 时,指出
时,指出 的单调递减区间和奇偶性(不需说明理由);
的单调递减区间和奇偶性(不需说明理由);
(2)当 时,求函数
时,求函数 的零点;
的零点;
(3)若对任何 不等式
不等式 恒成立,求实数
恒成立,求实数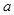 的取值范围。
的取值范围。
某企业生产某种商品 吨,此时所需生产费用为(
吨,此时所需生产费用为( )万元,当出售这种商品时,每吨价格为
)万元,当出售这种商品时,每吨价格为 万元,这里
万元,这里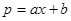 (
( 为常数,
为常数,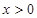 )
)
(1)为了使这种商品的生产费用平均每吨最低,那么这种商品的产量应为多少吨?
(2)如果生产出来的商品能全部卖完,当产量是120吨时企业利润最大,此时出售价格是每吨160万元,求 的值.
的值.
已知以角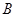 为钝角的的三角形
为钝角的的三角形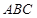 内角
内角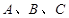 的对边分别为
的对边分别为 、
、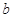 、
、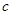 ,
,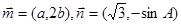 ,且
,且 与
与 垂直.
垂直.
(1)求角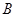 的大小;
的大小;
(2)求 的取值范围
的取值范围
在直三棱柱ABC-A1B1C1中,∠ABC=90°,AB=BC=1.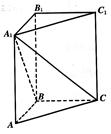
(1)求异面直线B1C1与AC所成角的大小;
(2)若该直三棱柱ABC-A1B1C1的体积为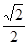 ,求点A到平面A1BC的距离.
,求点A到平面A1BC的距离.